日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（1）解不等式f（x）＞5；

（2）若存在實數x滿足ax+a≥f（x）成立，求實數a的取值范圍．

（1）以極點O為直角坐標原點，極軸為x軸正半軸建立平面直角坐標系，分別寫出直線l與曲線E的直角坐標方程；

（2）設直線l與曲線E交于A，B兩點，點C在曲線E上，求△ABC面積的最大值，并求此時點C的直角坐標．

【題目】已知函數f（x）＝ex．

（1）若f（x）的圖象在x＝a處切線的斜率為e﹣1，求正數a的值；

（2）對任意的a≥0，f（x）＞2lnxk恒成立，求整數k的最大值．

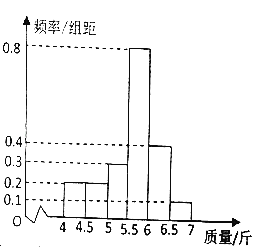
（1）現按分層抽樣的方法，從質量為[4.5，5），[5，5.5）的魚中隨機抽取5尾，再從這5尾中隨機抽取2尾，記隨機變量X表示質量在[4.5，5）內的魚的尾數，求X的分布列及數學期望．

（2）以各組數據的中間數代表這組數據的平均值，將頻率視為概率，該養殖戶還未捕撈的魚大約還有1000尾，現有兩個方案：

方案一：所有剩余的魚現在賣出，質量低于5.5斤的魚售價為每斤10元，質量高于5.5斤的魚售價為每斤12元

方案二：一周后所有剩余的魚逢節日賣出，假設每尾魚的質量不變，魚的數目不變，質量低于5.5斤的魚售價為每斤15元，這類魚養殖一周的費用是平均每尾22元；質量高于5.5斤的魚售價為每斤16元，這類魚養殖一周的費用是平均每尾24元通過計算確定水產養殖戶選擇哪種方案獲利更多？

【題目】已知雙曲線（a＞0，b＞0）的右焦點為F（3，0），左、右頂點分別為M，N，點P是E在第一象限上的任意一點，且滿足kPMkPN＝8．

（1）求雙曲線E的方程；

（2）若直線PN與雙曲線E的漸近線在第四象限的交點為A，且△PAF的面積不小于3，求直線PN的斜率k的取值范圍．

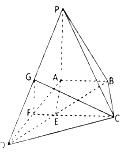
（1）若G為PD的中點，求證平面PAD⊥平面CGF；

（2）若AD＝AP＝6，求平面BCP與平面DCP所成銳二面角的余弦值．

【題目】已知數列{an}中，a1＝0，an+1＝an+6n+3，數列{bn}滿足bn＝n，則數列{bn}的最大項為第_____項

【題目】已知拋物線C1的頂點在坐標原點，準線為x＝﹣3，圓C2：（x﹣3）2+y2＝1，過圓心C2的直線l與拋物線C1交于點A，B，l與圓C2交于點M，N，且|AM|＜|AN|，則|AM||BM|的最小值為_____．

【題目】已知函數f（x）與g（x）＝3elnx+mx的圖象有4個不同的交點，則實數m的取值范圍是（ ）

A.（﹣3，）B.（﹣1，）C.（﹣1，3）D.（0，3）

A.1B.C.D.