
【題目】已知函數f(x)![]() 與g(x)=3elnx+mx的圖象有4個不同的交點,則實數m的取值范圍是( )
與g(x)=3elnx+mx的圖象有4個不同的交點,則實數m的取值范圍是( )
A.(﹣3,![]() )B.(﹣1,
)B.(﹣1,![]() )C.(﹣1,3)D.(0,3)
)C.(﹣1,3)D.(0,3)
科目:高中數學 來源: 題型:
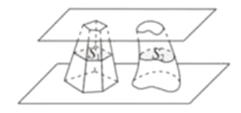
【題目】南北朝時代的偉大數學家祖暅在數學上有突出貢獻,他在實踐的基礎上提出祖暅原理:“冪勢既同,則積不容異”.其含義是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平面的任意平面所截,如果截得的兩個截面的面積總相等,那么這兩個幾何體的體積相等,如圖,夾在兩個平行平面之間的兩個幾何體的體積分別為![]() ,被平行于這兩個平面的任意平面截得的兩個截面的面積分別為
,被平行于這兩個平面的任意平面截得的兩個截面的面積分別為![]() ,則“
,則“![]() 總相等”是“
總相等”是“![]() 相等”的( )
相等”的( )
A.充分不必要條件B.必要不充分條件
C.充分必要條件D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,拋物線
,拋物線![]() 與圓
與圓![]() 的相交弦長為4.
的相交弦長為4.
(1)求拋物線![]() 的標準方程;
的標準方程;
(2)點![]() 為拋物線
為拋物線![]() 的焦點,
的焦點,![]() 為拋物線
為拋物線![]() 上兩點,
上兩點,![]() ,若
,若![]() 的面積為
的面積為![]() ,且直線
,且直線![]() 的斜率存在,求直線
的斜率存在,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健康社團為調查居民的運動情況,統計了某小區100名居民平均每天的運動時長(單位:小時)并根據統計數據分為![]() 六個小組(所調查的居民平均每天運動時長均在
六個小組(所調查的居民平均每天運動時長均在![]() 內),得到的頻率分布直方圖如圖所示.
內),得到的頻率分布直方圖如圖所示.
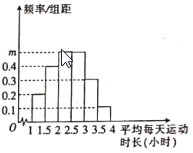
(1)求出圖中![]() 的值,并估計這
的值,并估計這![]() 名居民平均每天運動時長的平均值及中位數(同一組中的每個數據可用該組區間的中點值代替);
名居民平均每天運動時長的平均值及中位數(同一組中的每個數據可用該組區間的中點值代替);
(2)為了分析出該小區居民平均每天的運動量與職業、年齡等的關系,該社團按小組用分層抽樣的方法抽出20名居民進一步調查,試問在![]() 時間段內應抽出多少人?
時間段內應抽出多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水產養殖戶在魚成熟時,隨機從網箱中捕撈100尾魚,其質量分別在[4,4.5),[4.5.5),[5.5.5),[5.5,6),[6,6.5),[6.5,7](單位:斤)中,經統計得頻率分布直方圖如圖所示
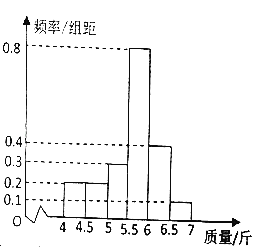
(1)現按分層抽樣的方法,從質量為[4.5,5),[5,5.5)的魚中隨機抽取5尾,再從這5尾中隨機抽取2尾,記隨機變量X表示質量在[4.5,5)內的魚的尾數,求X的分布列及數學期望.
(2)以各組數據的中間數代表這組數據的平均值,將頻率視為概率,該養殖戶還未捕撈的魚大約還有1000尾,現有兩個方案:
方案一:所有剩余的魚現在賣出,質量低于5.5斤的魚售價為每斤10元,質量高于5.5斤的魚售價為每斤12元
方案二:一周后所有剩余的魚逢節日賣出,假設每尾魚的質量不變,魚的數目不變,質量低于5.5斤的魚售價為每斤15元,這類魚養殖一周的費用是平均每尾22元;質量高于5.5斤的魚售價為每斤16元,這類魚養殖一周的費用是平均每尾24元通過計算確定水產養殖戶選擇哪種方案獲利更多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個三位數,個位、十位、百位上的數字依次為x,y,z,當且僅當y>x,y>z時,稱這樣的數為“凸數”(如243),現從集合{1,2,3,4}中取出三個不相同的數組成一個三位數,則這個三位數是“凸數”的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,點A(0,﹣3),點M滿足|MA|=2|MO|.
(1)求點M的軌跡方程;
(2)若圓C:(x﹣c)2+(y﹣c+1)2=1,判斷圓C上是否存在符合題意的M;
(3)設P(x1,y1),Q(x2,y2)是點M軌跡上的兩個動點,點P關于點(0,1)的對稱點為P1,點P關于直線y=1的對稱點為P2,如果直線QP1,QP2與y軸分別交于(0,a)和(0,b),問(a﹣1)(b﹣1)是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com