日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

【題目】我國古代在珠算發明之前多是用算籌為工具來記數、列式和計算的.算籌實際上是一根根相同長度的小木棍，如圖，算籌表示數1～9的方法有“縱式”和“橫式”兩種，規定個位數用縱式，十位數用橫式，百位數用縱式，千位數用橫式，萬位數用縱式，…，以此類推，交替使用縱橫兩式.例如：627可以表示為“”.如果用算籌表示一個不含“0”且沒有重復數字的三位數，這個數至少要用7根小木棍的概率為（ ）

A.B.C.D.

【題目】已知動圓與圓： 相切，且與圓： 相內切，記圓心的軌跡為曲線.設為曲線上的一個不在軸上的動點， 為坐標原點，過點作的平行線交曲線于, 兩個不同的點.

（Ⅰ）求曲線的方程；

（Ⅱ）試探究和的比值能否為一個常數？若能，求出這個常數，若不能，請說明理由；

（Ⅲ）記的面積為， 的面積為，令，求的最大值.

【題目】從某學校高三年級共1000名男生中隨機抽取50人測量身高，據測量，被測學生身高全部介于到之間，將測量結果按如下方式分成八組：第一組，第二組，…，第八組.如圖是按上述分組方法得到的頻率分布直方圖的一部分.其中第六組、第七組、第八組人數依次構成等差數列.

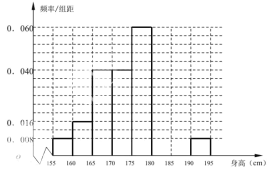
(1)求第六組、第七組的頻率，并估計高三年級全體男生身高在以上（含）的人數；

(2)學校決定讓這五十人在運動會上組成一個高旗隊，在這五十人中要選身高在以上（含）的兩人作為隊長，求這兩人在同一組的概率.

（1）求數列{an}的通項公式；

（2）設bn= ，求數列{bn}的前n項和Tn．

A. B. C. D.

（1）求實數a的值，并作出y＝f（x）的圖象；

（2）當m＞0，n＞0，且m+n＝2時，m2+n2≥f（x）恒成立，求實數x的取值范圍．

【題目】在平面直角坐標系xOy中，曲線C1的參數方程為（α為參數），曲線C2的參數方程為（β為參數）．以坐標原點O為極點，x軸的正半軸為極軸建立極坐標系．

（1）求曲線C1和C2的極坐標方程；

（2）若點A在曲線C1上，點B在曲線C2上，且∠AOB，求|OA||OB|的最大值．

【題目】已知函數f（x）a2x（k∈R，a＞0，e為自然對數的底數），且曲線f（x）在點（1，f（1））處的切線的斜率為e2﹣a2．

（1）求實數k的值，并討論函數f（x）的單調性；

（2）設函數g（x），若對x1∈（0，+∞），x2∈R，使不等式f（x2）≤g（x1）﹣1成立，求實數a的取值范圍．

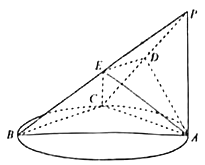
（1）求證：PC⊥平面ADE．

（2）若二面角C﹣AE﹣B為60°，求直線AB與平面ADE所成角的大小．

【題目】已知圓O：x2+y2＝3上的一動點M在x軸上的投影為N，點P滿足．

（1）求動點P的軌跡C的方程；

（2）若直線l與圓O相切，且交曲線C于點A，B，試求|AB|的最大值．