
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (α為參數),曲線C2的參數方程為
(α為參數),曲線C2的參數方程為![]() (β為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系.
(β為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系.
(1)求曲線C1和C2的極坐標方程;
(2)若點A在曲線C1上,點B在曲線C2上,且∠AOB![]() ,求|OA||OB|的最大值.
,求|OA||OB|的最大值.
【答案】(1)ρ=4cosθ,ρ=2cosθ.(2)4+2![]() .
.
【解析】
(1)利用![]() ,消去
,消去![]() 參數化為普通方程,再將直角坐標方程化為極坐標方程;
參數化為普通方程,再將直角坐標方程化為極坐標方程;
(2)設出![]() 的極坐標方程,利用極坐標意義可得出
的極坐標方程,利用極坐標意義可得出![]() ,運用三角恒等變換,化簡,即可求解.
,運用三角恒等變換,化簡,即可求解.
(1)曲線C1的參數方程為![]() (α為參數),
(α為參數),
消去參數α,可得直角坐標方程:(x﹣2)2+y2=4,
即x2+y2﹣4x=0,把x2+y2=ρ2,x=ρcosθ代入可得極坐標方程:
ρ2﹣4ρcosθ=0,即ρ=4cosθ.
曲線C2的參數方程為![]() (β為參數),
(β為參數),
消去參數β,可得直角坐標方程:(x﹣1)2+y2=1,
即x2+y2﹣2x=0,把x2+y2=ρ2,x=ρcosθ代入。
可得極坐標方程:ρ2﹣2ρcosθ=0,即ρ=2cosθ.
(2)若點A在曲線C1上,點B在曲線C2上,且∠AOB![]() ,
,
設![]()
則ρB=2cosθ,ρA=4cos(θ![]() )
)
則|OA||OB|=2cosθ×4cos(θ![]() )=8cosθ
)=8cosθ![]() (cosθ-sinθ)
(cosθ-sinθ)
=4![]() (cos2θ-sinθcosθ)=4
(cos2θ-sinθcosθ)=4![]()
![]() )
)
=4![]() +2
+2![]() .
.
∴![]() 時,|OA||OB|取得最大值4+2
時,|OA||OB|取得最大值4+2![]() .
.


科目:高中數學 來源: 題型:
【題目】已知一個口袋有m個白球,n個黑球(m,n![]()
![]() ,n
,n![]() 2),這些球除顏色外全部相同。現將口袋中的球隨機的逐個取出,并放入如圖所示的編號為1,2,3,……,m+n的抽屜內,其中第k次取球放入編號為k的抽屜(k=1,2,3,……,m+n).
2),這些球除顏色外全部相同。現將口袋中的球隨機的逐個取出,并放入如圖所示的編號為1,2,3,……,m+n的抽屜內,其中第k次取球放入編號為k的抽屜(k=1,2,3,……,m+n).
![]()
(1)試求編號為2的抽屜內放的是黑球的概率p;
(2)隨機變量x表示最后一個取出的黑球所在抽屜編號的倒數,E(x)是x的數學期望,證明 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在極坐標系中,O為極點,點![]() 在曲線
在曲線![]() 上,直線l過點
上,直線l過點![]() 且與
且與![]() 垂直,垂足為P.
垂直,垂足為P.
(1)當![]() 時,求
時,求![]() 及l的極坐標方程;
及l的極坐標方程;
(2)當M在C上運動且P在線段OM上時,求P點軌跡的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在△ABC中,角A,B,C所對的邊分別為a,b,c,其中A為銳角,且asin(B+C)是![]() bcosC與
bcosC與![]() ccosB的等差中項.
ccosB的等差中項.
(1)求角A的大小;
(2)若點D在△ABC的內部,且滿足∠CAD=∠ABD![]() ,∠CBD
,∠CBD![]() ,AD=1,求CD的長.
,AD=1,求CD的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與圓
與圓![]() :
: ![]() 相切,且與圓
相切,且與圓![]() :
: ![]() 相內切,記圓心
相內切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .設
.設![]() 為曲線
為曲線![]() 上的一個不在
上的一個不在![]() 軸上的動點,
軸上的動點, ![]() 為坐標原點,過點
為坐標原點,過點![]() 作
作![]() 的平行線交曲線
的平行線交曲線![]() 于
于![]() ,
, ![]() 兩個不同的點.
兩個不同的點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)試探究![]() 和
和![]() 的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
(Ⅲ)記![]() 的面積為
的面積為![]() ,
, ![]() 的面積為
的面積為![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某景區修建一棟復古建筑,其窗戶設計如圖所示.圓![]() 的圓心與矩形
的圓心與矩形![]() 對角線的交點重合,且圓與矩形上下兩邊相切(
對角線的交點重合,且圓與矩形上下兩邊相切(![]() 為上切點),與左右兩邊相交(
為上切點),與左右兩邊相交(![]() ,
,![]() 為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1
為其中兩個交點),圖中陰影部分為不透光區域,其余部分為透光區域.已知圓的半徑為1![]() ,且
,且![]() ,設
,設![]() ,透光區域的面積為
,透光區域的面積為![]() .
.
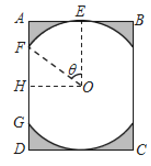
(1)求![]() 關于
關于![]() 的函數關系式,并求出定義域;
的函數關系式,并求出定義域;
(2)根據設計要求,透光區域與矩形窗面的面積比值越大越好.當該比值最大時,求邊![]() 的長度.
的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(I)在答題卡上作出這些數據的頻率分布直方圖:
(II)估計這種產品質量指標值的平均數及方差(同一組中的數據用該組區間的中點值作代表);
(III)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品的80%”的規定?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com