日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

如圖，五面體ABCDE中，正△ABC的邊長為1，AE⊥平面ABC，CD∥AE，且CD＝AE．

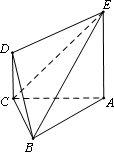
(Ⅰ)設CE與平面ABE所成的角為α，AE＝k(k＞0)，若α∈[，]，求k的取值范圍；

(Ⅱ)在(I)和條件下，當k取得最大值時，求平面BDE與平面ABC所成角的大小．

某地區試行高考考試改革：在高三學年中舉行5次統一測試，學生如果通過其中2次測試即可獲得足夠學分升上大學繼續學習，不用參加其余的測試，而每個學生最多也只能參加5次測試．假設某學生每次通過測試的概率都是1/3，每次測試通過與否互相獨立．規定：若前4次都沒有通過測試，則第5次不能參加測試

(1)求該學生考上大學的概率．

(2)記該生參加測試的次數為ξ，求ξ的分布列及ξ的數學期望．

在△ABC中，A，B，C的對邊分別為a，b，c，且acosC，bcosB，ccosA成等差數列．

(Ⅰ)求B的值；

(Ⅱ)求2sin²A＋cos(A－C)的范圍．

已知數列{a_n}中，a₁＝1，a₂＝，且a_n+1＝．(n＝2，3，4，…)．

(1)求a₃、a₄的值；

(2)設b_n＝－1(n∈N^*)，試用b_n表示b_n+1并求{a_n}的通項公式

(3)求證：對一切n∈N^*且n≥2，有a＋a＋…＋a＜．

已知函數f(x)＝x³＋3ax－1，g(x)＝(x)－ax－5，其中(x)是f(x)導函數

(Ⅰ)對滿足－1≤a≤1的一切a的值，都有g(x)＜0，求實數的取值范圍；

(Ⅱ)設a＝－m²，當實數m在什么范圍內變化時，函數y＝f(x)的圖象與直線y＝3只有一個公共點．

設數列{a_n}滿足a₁＋2a₂＋3a₃＋…＋na_n＝2ⁿ(n∈N^*)．

(Ⅰ)求數列{a_n}的通項；

(Ⅱ)設b_n＝n²a_n，求數列{b_n}的前n項和S_n．

如圖，五面體ABCDE中，正△ABC的邊長為1，AE⊥平面ABC，CD∥AE，且CD＝AE．

(Ⅰ)設CE與平面ABE所成的角為α，AE＝k(k＞0)，若α＝[，]，求k的取值范圍；

(Ⅱ)在(Ⅰ)和條件下，當k取得最大值時，求平面BDE與平面ABC所成角的大小．

某校2012年推優班報名正在進行，甲、乙、丙、丁四名學生躍躍欲試，現有四門學科(數學、物理、化學、信息技術)可供選擇，每位學生只能任選其中一科．

(1)求恰有兩門學科被選擇的概率；

(2)已知報名后，丁已指定被錄取．另外甲被錄取的概率為，乙被錄取的概率為，丙被錄取的概率為．求甲、乙、丙三人中至少有兩人被錄取的概率．

在△ABC中，A，B，C的對邊分別為a，b，c，且acosC，bcosB，ccosA成等差數列

(Ⅰ)求B的值；

(Ⅱ)求2sin²A＋cos(A－C)的范圍．

(理科)已知{a_n}是遞增數列，其前n項和為S_n，a₁＞1，且10S_n＝(2a_n＋1)(a_n＋2)，n∈N^*．

(Ⅰ)求數列{a_n}的通項a_n；

(Ⅱ)是否存在m，n，k∈N^*，使得2(a_m＋a_n)＝a_k成立？若存在，寫出一組符合條件的m，n，k的值；若不存在，請說明理由；

(Ⅲ)設，，若對于任意的n∈N^*，不等式恒成立，求正整數m的最大值．