
【題目】按如圖所示的程序框圖操作: (Ⅰ)寫出輸出的數(shù)所組成的數(shù)集.若將輸出的數(shù)按照輸出的順序從前往后依次排列,則得到數(shù)列{an},請寫出數(shù)列{an}的通項公式;
(Ⅱ)如何變更A框內的賦值語句,使得根據(jù)這個程序框圖所輸出的數(shù)恰好是數(shù)列{2n}的前7項?
(Ⅲ)如何變更B框內的賦值語句,使得根據(jù)這個程序框圖所輸出的數(shù)恰好是數(shù)列{3n﹣2}的前7項?
【答案】解:(Ⅰ)輸出的數(shù)組成的集合為{1,3,5,7,9,11,13}; 數(shù)列{an}的通項公式為an=2n﹣1(n∈N* , 且n≤7).
(Ⅱ)將A框內的語句改為“a=2”即可.
(Ⅲ)將B框內的語句改為“a=a+3”即可
【解析】(Ⅰ)由程序框圖可知,本題求一個數(shù)列的前7項,且這一數(shù)列首項為1,后面每一項比前面項多2,所以可得輸出的數(shù)組成的集合,并且此數(shù)列{an}恰為首項為1,公差為2的等差數(shù)列,再用等差數(shù)列通項公式即可求出數(shù)列{an}的通項公式(Ⅱ)要想使根據(jù)這個程序框圖所輸出的數(shù)恰好是數(shù)列{2n}的前7項,則前7項應為2,4,6,8,10,12,14,所以只需.將A框內的語句改為“a=2”即可.(Ⅲ)要想使根據(jù)這個程序框圖所輸出的數(shù)恰好是數(shù)列{3n﹣2}的前7項,則前7項應為1,4,7,10,13,16,19.只需將B框內的語句改為“a=a+3”即可.
【考點精析】通過靈活運用等差數(shù)列的前n項和公式和算法的循環(huán)結構,掌握前n項和公式:![]() ;在一些算法中,經常會出現(xiàn)從某處開始,按照一定條件,反復執(zhí)行某一處理步驟的情況,這就是循環(huán)結構,循環(huán)結構可細分為兩類:當型循環(huán)結構和直到型循環(huán)結構即可以解答此題.
;在一些算法中,經常會出現(xiàn)從某處開始,按照一定條件,反復執(zhí)行某一處理步驟的情況,這就是循環(huán)結構,循環(huán)結構可細分為兩類:當型循環(huán)結構和直到型循環(huán)結構即可以解答此題.


 高效智能課時作業(yè)系列答案
高效智能課時作業(yè)系列答案科目:高中數(shù)學 來源: 題型:
【題目】某商場欲經銷某種商品,考慮到不同顧客的喜好,決定同時銷售A、B兩個品牌,根據(jù)生產廠家營銷策略,結合本地區(qū)以往經銷該商品的大數(shù)據(jù)統(tǒng)計分析,A品牌的銷售利潤y1與投入資金x成正比,其關系如圖1所示,B品牌的銷售利潤y2與投入資金x的算術平方根成正比,其關系如圖2所示(利潤與資金的單位:萬元). 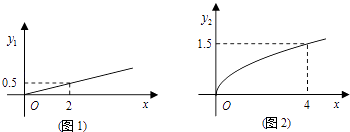
(1)分別將A、B兩個品牌的銷售利潤y1、y2表示為投入資金x的函數(shù)關系式;
(2)該商場計劃投入5萬元經銷該種商品,并全部投入A、B兩個品牌,問:怎樣分配這5萬元資金,才能使經銷該種商品獲得最大利潤,其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義在R上的可導函數(shù)f(x)的導函數(shù)為f′(x),滿足f′(x)>f(x),且f(x+2)為奇函數(shù),f(4)=﹣1,則不等式f(x)<ex的解集為( )
A.(﹣2,+∞)
B.(0,+∞)
C.(1,+∞)
D.(﹣∞,0)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() sinxcosx﹣cos2x+
sinxcosx﹣cos2x+ ![]() ,(x∈R).
,(x∈R).
(1)若對任意x∈[﹣ ![]() ,
, ![]() ],都有f(x)≥a,求a的取值范圍;
],都有f(x)≥a,求a的取值范圍;
(2)若先將y=f(x)的圖象上每個點縱坐標不變,橫坐標變?yōu)樵瓉淼?倍,然后再向左平移 ![]() 個單位得到函數(shù)y=g(x)的圖象,求函數(shù)y=g(x)﹣
個單位得到函數(shù)y=g(x)的圖象,求函數(shù)y=g(x)﹣ ![]() 在區(qū)間[﹣2π,4π]內的所有零點之和.
在區(qū)間[﹣2π,4π]內的所有零點之和.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】從2 012名學生中選取50名學生參加數(shù)學競賽,若采用下面的方法選取:先用簡單隨機抽樣從2 012人中剔除12人,剩下的2 000人再按系統(tǒng)抽樣的方法抽取50人,則在2 012人中,每人入選的概率( )
A.不全相等
B.均不相等
C.都相等,且為 ![]()
D.都相等,且為 ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若函數(shù)f(x)=1+ ![]() +sinx在區(qū)間[﹣k,k](k>0)上的值域為[m,n],則m+n=( )
+sinx在區(qū)間[﹣k,k](k>0)上的值域為[m,n],則m+n=( )
A.0
B.1
C.2
D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() ax2﹣(2a+1)x+2lnx(a∈R)
ax2﹣(2a+1)x+2lnx(a∈R)
(1)當a= ![]() 時,求函數(shù)f(x)的單調區(qū)間;
時,求函數(shù)f(x)的單調區(qū)間;
(2)設g(x)=(x2﹣2x)ex , 如果對任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立,求實數(shù)a的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com