如圖1,在直角梯形

中,

,

,

.將

沿
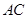
折起,使平面


平面

,得到幾何體

,如圖2所示.
(1)求證:

⊥平面

;(2)求幾何體

的體積.

(1)詳見解析
(2)幾何體

的體積為
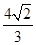
(1)在圖1中,可得
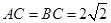
,從而
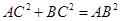
,故
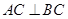
取
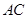
中點
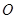
連結(jié)
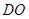
,則
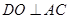
,又面


面

,
面

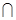
面

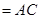
,
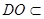
面

,從而
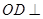
平面

,
∵
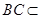
面

,∴
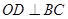
又
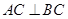
,
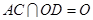
,
∴
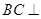
平面

解:在圖1中,可得
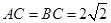
,從而
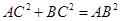
,故
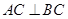
∵面


面

,面

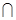
面

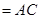
,
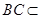
面

,從而
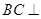
平面

(2)由(1)可知

為三棱錐
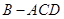
的高.
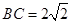
,
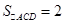
所以
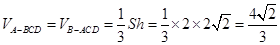
∴幾何體

的體積為
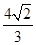
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,三棱錐

中,

平面

.

(1)求證:

平面

;
(2)若

,
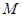
為

中點,求三棱錐
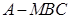
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知四棱柱的側(cè)棱長為2,且側(cè)棱垂直于底面,底面是邊長為2且有一個內(nèi)角為60°的菱形,若該四棱柱的俯視圖的面積與四棱柱的底面積相等,則該四棱柱左視圖面積的最小值是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知水平放置的△ABC的直觀圖△A′B′C′(斜二測畫法)是邊長為
a的正三角形,則原△ABC的面積為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知正三角形

的邊長為2,沿著

上的高

將正三角形折起,使得平面

平面
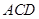
,則三棱錐

的體積是
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
一個半徑為1的小球在一個內(nèi)壁棱長為

的正四面體封閉容器內(nèi)可向各個方向自由運(yùn)動,則該小球表面永遠(yuǎn)不可能接觸到的容器內(nèi)壁的面積是
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
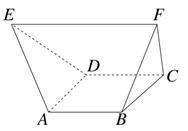
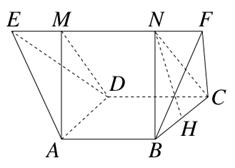
如圖,在多面體ABCDEF中,已知四邊形ABCD是邊長為1的正方形,且△ADE,△BCF均為正三角形,EF∥AB,EF=2,則該多面體的體積為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知三棱錐

中,

,

,直線
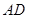
與底面
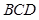
所成角為
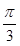
,則此時三棱錐外接球的表面積為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
圓柱M的底面直徑與高均等于球O的直徑,則圓柱M與球O的體積之比

.
查看答案和解析>>

 中,
中, ,
, ,
, .將
.將 沿
沿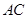 折起,使平面
折起,使平面
 平面
平面 ,得到幾何體
,得到幾何體 ,如圖2所示.
,如圖2所示. ⊥平面
⊥平面 ;(2)求幾何體
;(2)求幾何體 的體積.
的體積.

 的正四面體封閉容器內(nèi)可向各個方向自由運(yùn)動,則該小球表面永遠(yuǎn)不可能接觸到的容器內(nèi)壁的面積是 .
的正四面體封閉容器內(nèi)可向各個方向自由運(yùn)動,則該小球表面永遠(yuǎn)不可能接觸到的容器內(nèi)壁的面積是 . 




