
【題目】已知關于x的不等式(ax﹣a2﹣4)(x﹣4)>0的解集為A,且A中共含有n個整數,則當n最小時實數a的值為_____.
【答案】-2
【解析】
討論![]() 三種情況,a<0時,根據均值不等式得到a
三種情況,a<0時,根據均值不等式得到a![]() (﹣a
(﹣a![]() )≤﹣2
)≤﹣2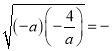 4,計算等號成立的條件得到答案.
4,計算等號成立的條件得到答案.
已知關于x的不等式(ax﹣a2﹣4)(x﹣4)>0,
①a<0時,[x﹣(a![]() )](x﹣4)<0,其中a
)](x﹣4)<0,其中a![]() 0,
0,
故解集為(a![]() ,4),
,4),
由于a![]() (﹣a
(﹣a![]() )≤﹣2
)≤﹣2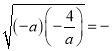 4,
4,
當且僅當﹣a![]() ,即a=﹣2時取等號,
,即a=﹣2時取等號,
∴a![]() 的最大值為﹣4,當且僅當a
的最大值為﹣4,當且僅當a![]() 4時,A中共含有最少個整數,此時實數a的值為﹣2;
4時,A中共含有最少個整數,此時實數a的值為﹣2;
②a=0時,﹣4(x﹣4)>0,解集為(﹣∞,4),整數解有無窮多,故a=0不符合條件;
③a>0時,[x﹣(a![]() )](x﹣4)>0,其中a
)](x﹣4)>0,其中a![]() 4,
4,
∴故解集為(﹣∞,4)∪(a![]() ,+∞),整數解有無窮多,故a>0不符合條件;
,+∞),整數解有無窮多,故a>0不符合條件;
綜上所述,a=﹣2.
故答案為:﹣2.


科目:高中數學 來源: 題型:
【題目】細葉青萎藤又稱海風藤,俗稱穿山龍,屬木質藤本植物,是我國常用大宗中藥材,以根莖入藥,具有舒筋活血、祛風止痛、止咳平喘、強身健體等醫療保健功效.通過研究光照、溫度和沙藏時間對細葉青萎藤種子萌發的影響,結果表明,細葉青萎藤種子發芽率和發芽指數均隨著沙藏時間的延長而提高.
下表給岀了2019年種植的一批試驗細葉青萎藤種子6組不同沙藏時間發芽的粒數.經計算:
沙藏時間 | 22 | 23 | 25 | 27 | 29 | 30 |
發芽數 | 8 | 11 | 20 | 30 | 59 | 70 |
![]() ,
,![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() 分別為試驗數據中的天數和發芽粒數,
分別為試驗數據中的天數和發芽粒數,![]() .
.
(1)求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (
(![]() 和
和![]() 都精確到0.01);
都精確到0.01);
(2)在題中的6組發芽的粒數不大于30的組數中,任意抽岀兩組,則這兩組數據中至少有一組滿足“![]() ”的概率是多少?
”的概率是多少?
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: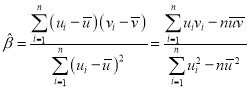 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() (
(![]() )的上頂點為
)的上頂點為![]() ,圓
,圓![]() 經過點
經過點![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 的垂線
的垂線![]() 交圓
交圓![]() 于另一點
于另一點![]() .若△PQN的面積為3,求直線
.若△PQN的面積為3,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查公司員工的飲食習慣與月收入之間的關系,隨機抽取了30名員工,并制作了這30人的月平均收入的頻率分布直方圖和飲食指數表(說明:圖中飲食指數低于70的人,飲食以蔬菜為主;飲食指數高于70的人,飲食以肉類為主).其中月收入4000元以上員工中有11人飲食指數高于70.
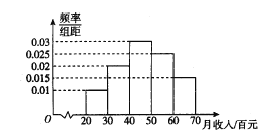
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
(1)是否有![]() 的把握認為飲食習慣與月收入有關系?若有,請說明理由,若沒有,說明理由并分析原因;
的把握認為飲食習慣與月收入有關系?若有,請說明理由,若沒有,說明理由并分析原因;
(2)從飲食指數在![]() 內的員工中任選2人,求他們的飲食指數均在
內的員工中任選2人,求他們的飲食指數均在![]() 內的概率;
內的概率;
(3)經調查某地若干戶家庭的年收入![]() (萬元)和年飲支出
(萬元)和年飲支出![]() (萬元)具有線性相關關系,并得到
(萬元)具有線性相關關系,并得到![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:![]() .若一個員工的月收入恰好為這30人的月平均收入,估計該人的年飲食支出費用.
.若一個員工的月收入恰好為這30人的月平均收入,估計該人的年飲食支出費用.
附: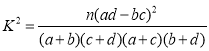 ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二面角α﹣l﹣β為60°,在其內部取點A,在半平面α,β內分別取點B,C.若點A到棱l的距離為1,則△ABC的周長的最小值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,兩座建筑物AB,CD的底部都在同一個水平面上,且均與水平面垂直,它們的高度分別是10m和20m,從建筑物AB的頂部A看建筑物CD的視角∠CAD=60°.
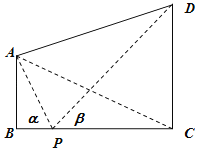
(1)求BC的長度;
(2)在線段BC上取一點P(點P與點B,C不重合),從點P看這兩座建筑物的視角分別為∠APB=α,∠DPC=β,問點P在何處時,α+β最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一直徑為8米的半圓形空地,現計劃種植甲、乙兩種水果,已知單位面積種植甲水果的經濟價值是種植乙水果經濟價值的5倍,但種植甲水果需要有輔助光照.半圓周上的![]() 處恰有一可旋轉光源滿足甲水果生長的需要,該光源照射范圍是
處恰有一可旋轉光源滿足甲水果生長的需要,該光源照射范圍是![]() ,點
,點![]() 在直徑
在直徑![]() 上,且
上,且![]() .
.

(1)若![]() 米,求
米,求![]() 的長;
的長;
(2)設![]() , 求該空地產生最大經濟價值時種植甲種水果的面積.
, 求該空地產生最大經濟價值時種植甲種水果的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年是中國改革開放的第40周年,為了充分認識新形勢下改革開放的時代性,某地的民調機構隨機選取了該地的100名市民進行調查,將他們的年齡分成6段:![]() ,并繪制了如圖所示的頻率分布直方圖.
,并繪制了如圖所示的頻率分布直方圖.
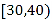
(1)現從年齡在![]() 內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用
內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用![]() 表示年齡在
表示年齡在![]() 內的人數,求
內的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若用樣本的頻率代替概率,用隨機抽樣的方法從該地抽取20名市民進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() .當
.當![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com