
分析 (1)通過討論x的范圍求出各個區間上的不等式的解集,取并集即可;
(2)因為存在x1∈R,存在x2∈R,使得f(x1)=g(x2)成立,所以{y|y=f(x),x∈R}∩{y|y=g(x),x∈R}≠∅,分別求出f(x),g(x)的范圍,即可求實數a的取值范圍.
解答 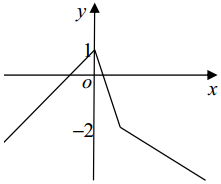 解:(1)由題意可得$g(x)=\left\{\begin{array}{l}1+x,x≤0\\ 1-3x,0<x<1\\-1-x,x≥1\end{array}\right.$
解:(1)由題意可得$g(x)=\left\{\begin{array}{l}1+x,x≤0\\ 1-3x,0<x<1\\-1-x,x≥1\end{array}\right.$
因為g(x)>-3,
由函數圖象可得不等式的解為-4<x<2,
所以不等式的解集為{x|-4<x<2}.
(2)因為存在x1∈R,存在x2∈R,使得f(x1)=g(x2)成立,
所以{y|y=f(x),x∈R}∩{y|y=g(x),x∈R}≠∅,
又f(x)=|4x-a|+|4x+3|≥|(4x-a)+(4x+3)|=|a+3|,
由(1)可知g(x)max=1,所以|a+3|≤1,解得-4≤a≤-2,
所以實數a的取值范圍為[-4,-2].
點評 本題考查了解絕對值不等式問題,考查集合的包含關系,是一道中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
| 是否愿意提供志愿者服務 性別 | 愿意 | 不愿意 |
| 男生 | 25 | 5 |
| 女生 | 15 | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
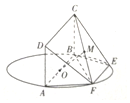 如圖,AB為圓O的直徑,點E,F在圓O上,AB∥EF,矩形ABCD所在的平面和圓(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如圖,AB為圓O的直徑,點E,F在圓O上,AB∥EF,矩形ABCD所在的平面和圓(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 18種 | B. | 24種 | C. | 36種 | D. | 48種 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com