
 如圖,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是線段BC上一動點,Q是線段DC上一動點,$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$,則$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值范圍是( )
如圖,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是線段BC上一動點,Q是線段DC上一動點,$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$,則$\overrightarrow{AP}$•$\overrightarrow{AQ}$的取值范圍是( )| A. | (-∞,$\frac{9}{4}$] | B. | [0,2] | C. | [0,3] | D. | [0,$\frac{9}{4}$] |
分析 建立如圖所示平面直角坐標系,得到相應點及向量的坐標,把$\overrightarrow{AP}$•$\overrightarrow{AQ}$利用數量積運算轉化為關于λ的函數求解.
解答 解:建立如圖所示平面直角坐標系,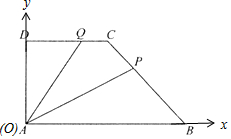
∵AB=2,AD=DC=1,
∴A(0,0),B(2,0),D(0,1),C(1,1),
∵$\overrightarrow{DQ}$=λ$\overrightarrow{DC}$,$\overrightarrow{CP}$=(1-λ)$\overrightarrow{CB}$,
∴$\overrightarrow{BP}=λ\overrightarrow{BC}$.
∴$\overrightarrow{AP}$•$\overrightarrow{AQ}$=($\overrightarrow{AB}+\overrightarrow{BP}$)•($\overrightarrow{AD}+\overrightarrow{DQ}$)
=($\overrightarrow{AB}+$$λ\overrightarrow{BC}$)•($\overrightarrow{AD}+λ\overrightarrow{DC}$)
=$\overrightarrow{AB}•\overrightarrow{AD}+λ\overrightarrow{AB}•\overrightarrow{DC}+λ\overrightarrow{BC}•\overrightarrow{AD}+{λ}^{2}\overrightarrow{BC}•\overrightarrow{DC}$
=$λ\overrightarrow{AB}•\overrightarrow{DC}+λ(\overrightarrow{AC}-\overrightarrow{AB})•\overrightarrow{AD}$+${λ}^{2}(\overrightarrow{AC}-\overrightarrow{AB})•\overrightarrow{DC}$
=$λ|\overrightarrow{AB}||\overrightarrow{DC}|cos0°+λ|\overrightarrow{AC}||\overrightarrow{AD}|cos45°$$+{λ}^{2}|\overrightarrow{AC}||\overrightarrow{DC}|cos45°$$-{λ}^{2}|\overrightarrow{AB}||\overrightarrow{DC}|cos0°$
=2λ+$\sqrt{2}×1×\frac{\sqrt{2}}{2}λ$$+\sqrt{2}×1×\frac{\sqrt{2}}{2}{λ}^{2}$-2λ2
=-λ2+3λ.
∵0≤λ≤1,∴$\overrightarrow{AP}$•$\overrightarrow{AQ}$=-λ2+3λ∈[0,2].
故選:B.
點評 本題考查平面向量的數量積運算,考查數學轉化思想方法,是中檔題.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在四棱錐P-ABCD中,側棱PA⊥平面ABCD,E為AD的中點,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1;
如圖,在四棱錐P-ABCD中,側棱PA⊥平面ABCD,E為AD的中點,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1;查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 兩個面平行,其余各面都是平行四邊形所圍成的幾何體一定是棱柱 | |
| B. | 若△ABC中,$\overrightarrow{AB}$•$\overrightarrow{BC}$<0,則△ABC是鈍角三角形 | |
| C. | 函數f(x)=x+$\frac{4}{x-1}$(x>1)的最小值為5 | |
| D. | 若G2=ab,則G是a,b的等比中項 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com