【題目】已知
，
為
個不同的冪函數，有下列命題：
① 函數
必過定點
；
② 函數可能過點
；
③ 若
，則函數
為偶函數；
④ 對于任意的一組數
、
、…、
，一定存在各不相同的
個數
、
、…、
使得
在
上為增函數.其中真命題的個數為（ ）
A.1個B.2個C.3個D.4個
【答案】A
【解析】
根據題目中的條件和冪函數的圖像與性質，對四個命題分別進行判斷，從而得到答案.
命題①，因為
，
為
個不同的冪函數，
且冪函數都經過點
，
所以可得函數
的圖像一定過點
，所以正確;
命題②，冪函數，若定義域中可取負數時，則冪函數圖像一定過
或者
，為個不同的冪函數，
若這個不同的冪函數都過，則函數的圖像過
，
若這個不同的冪函數有一個不過，則這個冪函數必過，則函數的圖像過
，
所以的圖像不可能過
，所以錯誤；
命題③若
，若
這個數中出現分子為奇數，分母為偶數的分數，則函數
的定義域為
，不關于原點對稱，所以函數不為偶函數，所以錯誤.
命題④因為任意的一組數
、
、…、
，一定存在各不相同的
個數
、
、…、
，
則當這個數中出現
時，
，此時
為常數函數，不是增函數，所以錯誤.
故選：A.
科目：高中數學 來源： 題型：
【題目】下列命題錯誤的是（ ）
A. 命題“若
，則
”的逆否命題為“若
，則
”
B. 若
為假命題，則
均為假命題
C. 對于命題
：
，使得
，則
：
，均有
D. “
”是“
”的充分不必要條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
且
．
（1）求實數
的值；
（2）判斷函數
在區間
上的單調性，并用函數單調性的定義證明；
（3）求實數
的取值范圍，使得關于
的方程
分別為：
①有且僅有一個實數解；②有兩個不同的實數解；③有三個不同的實數解．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】臨近2020年春節，西寧市各賣場挖空心思尋找促銷策略.商人張三豐善于運用數學思維進行銷售分析，他根據以往當地的需求情況，得出如下他所經營的某種產品日需求量的頻率分布直方圖.
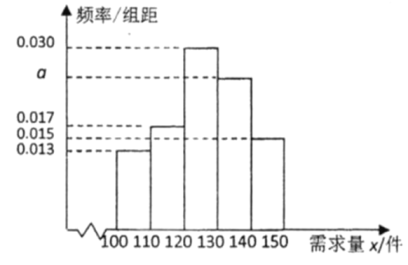
（1）求圖中
的值，并估計日需求量的眾數:
（2）某日，張三豐購進130件該種產品，根據近期市場行情，當天每售出1件能獲利30元，未售出的部分，每件虧損20元設當天的需求量為
件
，純利潤為
元
（i）將表示為的函數；（ii）根據直方圖估計當天純利潤不少于3400元的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于定義在區間
的函數
，定義：
（
），
（），其中，
表示函數在
上的最小值，
表示函數在上的最大值.
（1）若
，
，試寫出
、
的表達式；
（2）設
且
，函數
，
，如果與恰好為同一函數，求
的取值范圍.
（3）若存在最小正整數
，使得
對任意的成立，則稱函數為上的“階收縮函數”，已知函數
，
，試判斷是否為
上的“階收縮函數”，如果是，求出對應的，如果不是，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
（1）求
的取值范圍，使
在閉區間
上存在反函數；
（2）當
時，函數的最小值是關于的函數
，求的最大值及其相應的值；
（3）對于，研究函數的圖像與函數
的圖像公共點的個數，并寫出公共點的橫坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（其中
，
，
，
是實數常數，
）.
（1）若
，函數
的圖象關于點
成中心對稱，求，的值；
（2）若函數滿足條件（1），且對任意
，總有
，求的取值范圍；
（3）若
，函數是奇函數，
，
，且對任意
時，不等式
恒成立，求負實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】拋物線C的頂點在坐標原點，對稱軸為x軸，拋物線C過點A（4，4），過拋物線C的焦點F作傾斜角等于45°的直線l，直線l交拋物線C于M、N兩點．
（1）求拋物線C的方程；
（2）求線段MN的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
