
【題目】已知函數![]() ,其中a,
,其中a,![]() .
.
(1)當![]() ,
,![]() 時,求函數
時,求函數![]() 的零點;
的零點;
(2)當![]() 時,解關于x的不等式
時,解關于x的不等式![]() ;
;
(3)如果函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的上方,證明:
的上方,證明:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)當
;(2)當![]() 時,解集為
時,解集為![]() ,當
,當![]() 時解集為
時解集為![]() ,當
,當![]() 時,解集為
時,解集為![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)將![]() ,
,![]() 代入函數得
代入函數得 ![]() ,,令
,,令![]() ,解方程即可求得函數的零點;
,解方程即可求得函數的零點;
(2)將![]() 代入函數得
代入函數得 ![]() ,令
,令![]() 解得
解得![]() 或
或![]() ,分
,分![]() 、
、![]() 、
、![]() 三種情況討論
三種情況討論![]() 的解集即可.
的解集即可.
(3)根據函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的上方,得
的上方,得![]() 對任意的
對任意的![]() 恒成立,即
恒成立,即![]() 對任意的
對任意的![]() 恒成立, 則函數圖象與
恒成立, 則函數圖象與![]() 軸無交點,
軸無交點,![]() ,即
,即![]() ,又因為
,又因為![]() ,所以
,所以![]() ,
,![]() .
.
解: (1)因為函數![]() ,
,
當![]() ,
,![]() 時,
時, ![]()
![]() ,則
,則![]() ,解得
,解得![]() 或
或![]() .
.
所以函數的零點為![]() 或
或![]() ;
;
(2)當![]() 時,
時, ![]() ,
,
令![]() 解得
解得![]() 或
或![]() ,
,
①當![]() 時,
時, ![]() 的解集為
的解集為![]()
②當![]() 時,
時, ![]() 的解集為
的解集為![]() ,
,
③當![]() 時,
時, ![]() 的解集為
的解集為![]() .
.
(3)如果函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的上方,
的上方,
則![]() 對任意的
對任意的![]() 恒成立,
恒成立,
即![]() 對任意的
對任意的![]() 恒成立
恒成立
![]() ,即
,即![]()
又因為![]() ,所以
,所以![]() ,
,![]() .
.
所以函數![]() 的圖象恒在直線
的圖象恒在直線![]() 的上方,
的上方, ![]() 成立.
成立.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】2018年8月8日是我國第十個全民健身日,其主題是:新時代全民健身動起來。某市為了解全民健身情況,隨機從某小區居民中抽取了40人,將他們的年齡分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如圖所示的頻率分布直方圖。
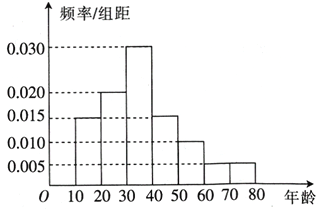
(1)試求這40人年齡的平均數、中位數的估計值;
(2)(i)若從樣本中年齡在[50,70)的居民中任取2人贈送健身卡,求這2人中至少有1人年齡不低于60歲的概率;
(ⅱ)已知該小區年齡在[10,80]內的總人數為2000,若18歲以上(含18歲)為成年人,試估計該小區年齡不超過80歲的成年人人數。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】信息科技的進步和互聯網商業模式的興起,全方位地改變了大家金融消費的習慣和金融交易模式,現在銀行的大部分業務都可以通過智能終端設備完成,多家銀行職員人數在悄然減少.某銀行現有職員320人,平均每人每年可創利20萬元.據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年多創利0.2萬元,但銀行需付下崗職員每人每年6萬元的生活費,并且該銀行正常運轉所需人數不得小于現有職員的![]() ,為使裁員后獲得的經濟效益最大,該銀行應裁員多少人?此時銀行所獲得的最大經濟效益是多少萬元?
,為使裁員后獲得的經濟效益最大,該銀行應裁員多少人?此時銀行所獲得的最大經濟效益是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《數書九章》是中國南宋時期杰出數學家秦九韶的著作,其中在卷五“三斜求積”中提出了已知三角形三邊![]() 、
、![]() 、
、![]() ,求面積的公式,這與古希臘的海倫公式完全等價,其求法是“以小斜冥并大斜冥減中斜冥,余半之,自乘于上,以小斜冥乘大斜冥減上,余四約之,為實.一為從隅,開平方得積”若把以上這段文字寫出公式,即若
,求面積的公式,這與古希臘的海倫公式完全等價,其求法是“以小斜冥并大斜冥減中斜冥,余半之,自乘于上,以小斜冥乘大斜冥減上,余四約之,為實.一為從隅,開平方得積”若把以上這段文字寫出公式,即若![]() ,則
,則![]() .
.
(1)已知![]() 的三邊
的三邊![]() ,
,![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() 的面積
的面積![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐的頂點為![]() ,底面圓心為
,底面圓心為![]() ,半徑為
,半徑為![]() .
.
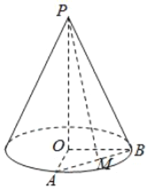
(1)設圓錐的母線長為![]() ,求圓錐的體積;
,求圓錐的體積;
(2)設![]() ,
,![]() 、
、![]() 是底面半徑,且
是底面半徑,且![]() ,
,![]() 為線段
為線段![]() 的中點,如圖.求異面直線
的中點,如圖.求異面直線![]() 與
與![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AOB是一塊半徑為r的扇形空地,![]() .某單位計劃在空地上修建一個矩形的活動場地OCDE及一矩形停車場EFGH,剩余的地方進行綠化.若
.某單位計劃在空地上修建一個矩形的活動場地OCDE及一矩形停車場EFGH,剩余的地方進行綠化.若![]() ,設
,設![]()
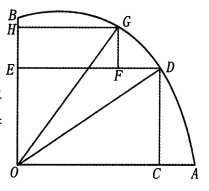
(Ⅰ)記活動場地與停車場占地總面積為![]() ,求
,求![]() 的表達式;
的表達式;
(Ⅱ)當![]() 為何值時,可使活動場地與停車場占地總面積最大.
為何值時,可使活動場地與停車場占地總面積最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,設點
中,設點![]() ,直線
,直線![]() :
:![]() ,點
,點![]() 在直線
在直線![]() 上移動,
上移動,![]() 是線段
是線段![]() 與
與![]() 軸的交點,過
軸的交點,過![]() 、
、![]() 分別作直線
分別作直線![]() 、
、![]() ,使
,使![]() ,
,![]() ,
,![]() .
.
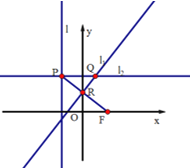
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知⊙![]() :
:![]() ,過拋物線
,過拋物線![]() 上一點
上一點![]() 作兩條直線與⊙
作兩條直線與⊙![]() 相切于
相切于![]() 、
、![]() 兩點,若直線
兩點,若直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com