
【題目】如圖,在平面直角坐標系![]() 中,設點
中,設點![]() ,直線
,直線![]() :
:![]() ,點
,點![]() 在直線
在直線![]() 上移動,
上移動,![]() 是線段
是線段![]() 與
與![]() 軸的交點,過
軸的交點,過![]() 、
、![]() 分別作直線
分別作直線![]() 、
、![]() ,使
,使![]() ,
,![]() ,
,![]() .
.
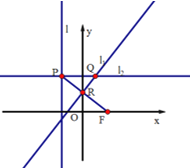
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知⊙![]() :
:![]() ,過拋物線
,過拋物線![]() 上一點
上一點![]() 作兩條直線與⊙
作兩條直線與⊙![]() 相切于
相切于![]() 、
、![]() 兩點,若直線
兩點,若直線![]() 在
在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的最小值.
的最小值.
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝所著的![]() 詳解九章算術
詳解九章算術![]() 一書中,用圖
一書中,用圖![]() 的數表列出了一些正整數在三角形中的一種幾何排列,俗稱“楊輝三角形”,該數表的規律是每行首尾數字均為1,從第三行開始,其余的數字是它“上方”左右兩個數字之和
的數表列出了一些正整數在三角形中的一種幾何排列,俗稱“楊輝三角形”,該數表的規律是每行首尾數字均為1,從第三行開始,其余的數字是它“上方”左右兩個數字之和![]() 現將楊輝三角形中的奇數換成1,偶數換成0,得到圖
現將楊輝三角形中的奇數換成1,偶數換成0,得到圖![]() 所示的由數字0和1組成的三角形數表,由上往下數,記第n行各數字的和為
所示的由數字0和1組成的三角形數表,由上往下數,記第n行各數字的和為![]() ,如
,如![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]()
![]()

A. 2 B. 4 C. 8 D. 16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某批發市場一服裝店試銷一種成本為每件![]() 元的服裝規定試銷期間銷售單價不低于成本單價,且獲利不得高于成本的
元的服裝規定試銷期間銷售單價不低于成本單價,且獲利不得高于成本的![]() ,經試銷發現銷售量
,經試銷發現銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)符合一次函數
(元)符合一次函數![]() ,且
,且![]() 時,
時,![]() ;
;![]() 時,
時,![]() .
.
(1)求一次函數![]() 的解析式,并指出
的解析式,并指出![]() 的取值范圍;
的取值范圍;
(2)若該服裝店獲得利潤為![]() 元,試寫出利潤
元,試寫出利潤![]() 與銷售單價
與銷售單價![]() 之間的關系式;銷售單價
之間的關系式;銷售單價![]() 定為多少元時,可獲得最大利潤最大利潤是多少元?
定為多少元時,可獲得最大利潤最大利潤是多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市的公交公司為了方便市民出行,科學規劃車輛投放,在一個人員密集流動地段增設一個起點站,為了研究車輛發車間隔時間![]() 與乘客等候人數
與乘客等候人數![]() 之間的關系,經過調查得到如下數據:
之間的關系,經過調查得到如下數據:
間隔時間/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人數y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
調查小組先從這![]() 組數據中選取
組數據中選取![]() 組數據求線性回歸方程,再用剩下的
組數據求線性回歸方程,再用剩下的![]() 組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數
組數據進行檢驗.檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數
與實際等候人數![]() 的差,若差值的絕對值都不超過
的差,若差值的絕對值都不超過![]() ,則稱所求方程是“恰當回歸方程”.
,則稱所求方程是“恰當回歸方程”.
(1)從這![]() 組數據中隨機選取2組數據,求選取的這
組數據中隨機選取2組數據,求選取的這![]() 組數據的間隔時間不相鄰的概率;
組數據的間隔時間不相鄰的概率;
(2)若選取的是后面![]() 組數據,求
組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判斷此方程是否是“恰當回歸方程”;
,并判斷此方程是否是“恰當回歸方程”;
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
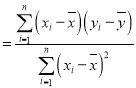 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知橢圓![]() 過點
過點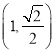 ,離心率為
,離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,點
,點![]() 為直線
為直線![]() 上且不在
上且不在![]() 軸上的任意一點,直線
軸上的任意一點,直線![]() 和
和![]() 與橢圓的交點分別為
與橢圓的交點分別為![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 為坐標原點.
為坐標原點.
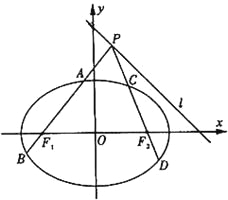
(1)求橢圓的標準方程;
(2)設直線![]() 、
、![]() 的斜線分別為
的斜線分別為![]() 、
、![]() .
.
(i)證明:![]() ;
;
(ii)問直線![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 、
、![]() 、
、![]() 、
、![]() 的斜率
的斜率![]() 、
、![]() 、
、![]() 、
、![]() 滿足
滿足![]() ?若存在,求出所有滿足條件的點
?若存在,求出所有滿足條件的點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數y=f1(x)的圖象以原點為頂點且過點(1,1),反比例函數y=f2(x)的圖象與直線y=x的兩個交點間距離為8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函數f(x)的表達式;
(Ⅱ) 證明:當a>3時,關于x的方程f(x)= f(a)有三個實數解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工藝公司要對某種工藝品深加工,已知每個工藝品進價為20元,每個的加工費為n元,銷售單價為x元.根據市場調查,須有![]() ,
,![]() ,
,![]() ,同時日銷售量m(單位:個)與
,同時日銷售量m(單位:個)與![]() 成正比.當每個工藝品的銷售單價為29元時,日銷售量為1000個.
成正比.當每個工藝品的銷售單價為29元時,日銷售量為1000個.
(1)寫出日銷售利潤y(單位:元)與x的函數關系式;
(2)當每個工藝品的加工費用為5元時,要使該公司的日銷售利潤為100萬元,試確定銷售單價x的值.(提示:函數![]() 與
與![]() 的圖象在
的圖象在![]() 上有且只有一個公共點)
上有且只有一個公共點)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com