
【題目】2018年8月8日是我國第十個全民健身日,其主題是:新時代全民健身動起來。某市為了解全民健身情況,隨機從某小區居民中抽取了40人,將他們的年齡分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如圖所示的頻率分布直方圖。
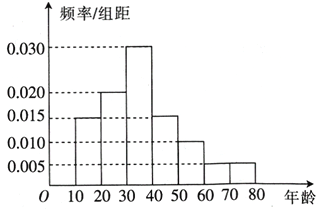
(1)試求這40人年齡的平均數、中位數的估計值;
(2)(i)若從樣本中年齡在[50,70)的居民中任取2人贈送健身卡,求這2人中至少有1人年齡不低于60歲的概率;
(ⅱ)已知該小區年齡在[10,80]內的總人數為2000,若18歲以上(含18歲)為成年人,試估計該小區年齡不超過80歲的成年人人數。
【答案】(1) 平均數37,中位數為35;(2) (ⅰ)![]() ;(ⅱ)該小區年齡不超過80歲的成年人人數約為2000×0.88=1760.
;(ⅱ)該小區年齡不超過80歲的成年人人數約為2000×0.88=1760.
【解析】
(1)每個矩形的中點橫坐標與該矩形的縱坐標相乘后求和可得平均值;直方圖左右兩邊面積相等處橫坐標表示中位數;(2)(ⅰ)從6人中任選2人共有15個基本事件,至少有1人年齡不低于60歲的共有9個基本事件,由古典概型概率公式可得結果;(ⅱ)樣本中年齡在18歲以上的居民所占頻率為1-(18-10)×0.015=0.88.
(1)平均數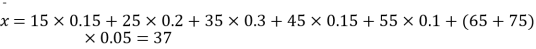 .
.
前三組的頻率之和為0.15+0.2+0.3=0.65,故中位數落在第3組,設中位數為x,
則(x-30)×0.03+0.15+0.2=0.5,解得x=35,即中位數為35.
(2)(ⅰ)樣本中,年齡在[50,70)的人共有40×0.15=6人,其中年齡在[50,60)的有4人,設為a,b,c,d,年齡在[60,70)的有2人,設為x,y.
則從中任選2人共有如下15個基本事件:(a,b),(a,c),(a,d),(a,x),(a,y),(b,c),(b,d),(b,x),(b,y),(c,d),(c,x),(c,y),(d,x),(d,y),(x,y).
至少有1人年齡不低于60歲的共有如下9個基本事件:
(a,x),(a,y),(b,x),(b,y),(c,x),(c,y),(d,x),(d,y),(x,y).
記“這2人中至少有1人年齡不低于60歲”為事件A,
故所求概率![]() .
.
(ⅱ)樣本中年齡在18歲以上的居民所占頻率為1-(18-10)×0.015=0.88,
故可以估計,該小區年齡不超過80歲的成年人人數約為2000×0.88=1760.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,![]() 是圓柱的直徑,
是圓柱的直徑,![]() 是圓柱的母線,
是圓柱的母線,![]() ,
,![]() ,點
,點![]() 是圓柱底面圓周上的點.
是圓柱底面圓周上的點.
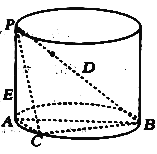
(1)求三棱錐![]() 體積的最大值;
體積的最大值;
(2)若![]() ,
,![]() 是線段
是線段![]() 上靠近點
上靠近點![]() 的三等分點,點
的三等分點,點![]() 是線段
是線段![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]()

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱錐P-ABCD的體積為
,且四棱錐P-ABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩點![]() 、
、![]() ,動點
,動點![]() 在
在![]() 軸上的射影是
軸上的射影是![]() ,且
,且![]() .
.
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)設直線![]() 、
、![]() 的兩個斜率存在,分別記為
的兩個斜率存在,分別記為![]() 、
、![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)若經過點![]() 的直線
的直線![]() 與動點
與動點![]() 的軌跡有兩個交點
的軌跡有兩個交點![]() 、
、![]() ,當
,當![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .以極點為原點,極軸為
.以極點為原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)判斷直線![]() 與曲線
與曲線![]() 的位置關系,并說明理由;
的位置關系,并說明理由;
(2)若直線![]() 和曲線
和曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com