Question

7．三棱錐P-ABC中，面PBC和面ABC都是邊長為12的正三角形，平面PBC和平面ABC所成二面角是60°，求點P到平面ABC的距離．

Answer 1

分析 取BC的中點D，連接AD、PD．則PD垂直BC、AD垂直BC，∠PDA為二面角的平面角，作PE⊥AD于E．因為BC⊥平面ADP，所以BC⊥PE，故PE⊥平面ABC，從而PE即為所求距離．

解答 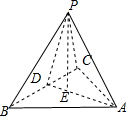解：取BC的中點D，連接AD、PD．則PD垂直BC、AD垂直BC，
∴∠PDA為二面角的平面角，故∠PDA=60°．
作PE⊥AD于E．因為BC⊥平面ADP，所以BC⊥PE，故PE⊥平面ABC，
從而PE即為所求距離．
求得：PD=6$\sqrt{3}$，所以PE=PD$•\frac{\sqrt{3}}{2}$=9．

點評 本題考查點面距離的計算，考查二面角，考查學生分析解決問題的能力，屬于中檔題．