Question

8．已知函數f（x）=xlnx-$\frac{a}{2}$x²-x+a（a∈R）．
（Ⅰ）當a=0時，求f（x）的單調區間；
（Ⅱ）若函數f（x）在其定義域內有兩個不同的極值點．
（ⅰ）求a的取值范圍；
（ⅱ）設兩個極值點分別為x₁，x₂，證明：x₁•x₂＞e²．

Answer 1

分析 （Ⅰ）對f（x）求導，利用導數來判斷f（x）的圖形單調性；
（Ⅱ）（i）函數f（x）在其定義域內有兩個不同的極值點轉化為：方程lnx-ax=0在x＞0上有兩個不同根．
（ii）x₁，x₂分別是方程lnx-ax=0的兩個根，即lnx₁=ax₁，lnx₂=ax₂；不妨設x₁＞x₂，作差得，ln$\frac{{x}_{1}}{{x}_{2}}$=a（x₁-x₂），即a=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$．原不等式${x_1}•{x_2}＞{e^2}$等價于$ln{x_1}+ln{x_2}＞2?a（{{x_1}+{x_2}}）＞2?ln\frac{x_1}{x_2}＞\frac{{2（{{x_1}-{x_2}}）}}{{{x_1}+{x_2}}}$．

解答 解：（Ⅰ）當a=0時，f（x）=xlnx-x．
函數f（x）的定義域為x＞0，f'（x）=lnx；
當x＞1時，f'（x）＞0；當0＜x＜1時，f'（x）＜0．
所以，f（x）在（0，1）上單調遞減；在（1，+∞）上單調遞增．
（Ⅱ） （ⅰ）依題意，函數f（x）的定義域為x＞0，f'（x）=lnx-ax
所以方程f'（x）=0在x＞0上有兩個不同根，即：
方程lnx-ax=0在x＞0上有兩個不同根，轉化為：函數y=lnx與函數y=ax
的圖象在x＞0上有兩個不同交點，如圖．
可見，若令過原點且切于函數y=lnx圖象的直線斜率為k，只須0＜a＜k．
令切點A（x₀，lnx₀），所以k=$\frac{1}{{x}_{0}}$，又k=$\frac{ln{x}_{0}}{{x}_{0}}$，所以$\frac{1}{{x}_{0}}=\frac{ln{x}_{0}}{{x}_{0}}$，
解得：x₀=e，于是k=$\frac{1}{e}$，
所以，0＜a＜$\frac{1}{e}$．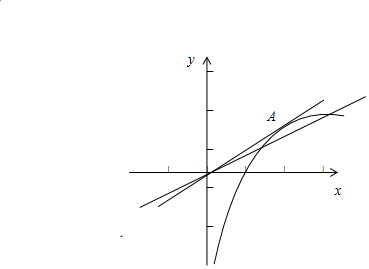
（ⅱ）由（i）可知x₁，x₂分別是方程lnx-ax=0的兩個根，
即lnx₁=ax₁，lnx₂=ax₂，
不妨設x₁＞x₂，作差得，ln$\frac{{x}_{1}}{{x}_{2}}$=a（x₁-x₂），即a=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$．
原不等式${x_1}•{x_2}＞{e^2}$
等價于$ln{x_1}+ln{x_2}＞2?a（{{x_1}+{x_2}}）＞2?ln\frac{x_1}{x_2}＞\frac{{2（{{x_1}-{x_2}}）}}{{{x_1}+{x_2}}}$
令$\frac{x_1}{x_2}=t$，則t＞1，$ln\frac{x_1}{x_2}＞\frac{{2（{{x_1}-{x_2}}）}}{{{x_1}+{x_2}}}?lnt＞\frac{{2（{t-1}）}}{t+1}$
設$g（t）=lnt-\frac{{2（{t-1}）}}{t+1}，t＞1$，$g'（t）=\frac{{{{（{t-1}）}^2}}}{{t{{（{t+1}）}^2}}}＞0$，
∴函數g（t）在（1，+∞）上單調遞增，
∴g（t）＞g（1）=0，
即不等式$lnt＞\frac{{2（{t-1}）}}{t+1}$成立，
故所證不等式${x_1}•{x_2}＞{e^2}$成立．

點評 本題主要考查了導數研究函數的單調性，方程與函數思想，轉化思想，屬中等題．