【題目】在直角坐標系
中，曲線
上的點均在曲線
外，且對上任意一點
，到直線
的距離等于該點與曲線
上點的距離的最小值．
（1）求動點的軌跡的方程；
（2）若點
是曲線的焦點，過的兩條直線
關于
軸對稱，且分別交曲線于
，若四邊形
的面積等于
，求直線的方程.
【答案】（1）
；（2）
.
【解析】
（1）求得
的圓心和半徑，利用題目所給“
到直線
的距離等于該點與曲線上點的距離的最小值”列方程，化簡這個方程可求得軌跡
的方程.（2）設出直線
的方程，代入拋物線的方程求得弦長
的值.根據對稱性求得
的值，利用面積公式列方程，從而求得所求直線的斜率，進而求得直線方程.
（1）由已知得曲線是以
為圓心，
為半徑的圓.設
，則到直線
的距離等于
，又到圓上的點的距離的最小值為
，所以由已知可得
，化簡得， 所以曲線的方程為.（2）依題意可知，直線
的斜率存在，并且互為相反數.設直線
的方程
，代入拋物線方程并化簡得
，故
，由弦長公式得
，同理
.下面求直線夾角的正弦值.設直線的傾斜角為
，則
，則直線夾角為
，且
.所以四邊形
的面積為
，
，解得
，此時直線
的斜率為
，根據對稱性可知.當直線斜率為
時，斜率為，也符合題意.故
，所求的直線方程為.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P-ABC中，
底面ABC，
.點D，E，N分別為棱PA，PC，BC的中點，M是線段AD的中點，
，
.
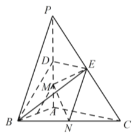
（1）求證：
平面BDE；
（2）求二面角C-EM-N的正弦值.
（3）已知點H在棱PA上，且直線NH與直線BE所成角的余弦值為
，求線段AH的長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某網站針對“2016年春節放假安排”開展網上問卷調查，提出了A，B兩種放假方案，調查結果如表：(單位：萬人)
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 | n |
已知從所有參與調查的人中任選1人是“老年人”的概率為
.
(1)求n的值；
(2)從參與調查的“老年人”中，用分層抽樣的方法抽取6人，在這6人中任意選取2人，求恰好有1人“支持B方案”的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從4名書法比賽一等獎的同學和2名繪畫比賽一等獎的同學中選出2名志愿者，參加某項服務工作.
(1)求選出的兩名志愿者都是獲得書法比賽一等獎的同學的概率；
(2)求選出的兩名志愿者中一名是獲得書法比賽一等獎，另一名是獲得繪畫比賽一等獎的同學的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知梯形
如圖（1）所示，其中
， 
，四邊形
是邊長為
的正方形，現沿
進行折疊，使得平面
平面
，得到如圖（2）所示的幾何體.
（Ⅰ）求證：平面
平面
；
（Ⅱ）已知點
在線段
上，且
平面
，求
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校一位教師要去某地參加全國數學優質課比賽，已知他乘火車、輪船、汽車、飛機直接去的概率分別為0.3、0.1、0.2、0.4.
（1）求他乘火車或乘飛機去的概率；
（2）他不乘輪船去的概率；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數據
是鄭州市普通職工
個人的年收入，若這
個數據的中位數為
，平均數為
，方差為
，如果再加上世界首富的年收入
，則這
個數據中，下列說法正確的是（ ）
A.年收入平均數大大增大，中位數一定變大，方差可能不變
B.年收入平均數大大增大，中位數可能不變，方差變大
C.年收入平均數大大增大，中位數可能不變，方差也不變
D.年收入平均數可能不變，中位數可能不變，方差可能不變
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某投資公司計劃在甲、乙兩個互聯網創新項目上共投資1200萬元，每個項目至少要投資300萬元.根據市場分析預測：甲項目的收益
與投入
滿足
，乙項目的收益
與投入滿足
.設甲項目的投入為
.
（1）求兩個項目的總收益關于的函數
.
（2）如何安排甲、乙兩個項目的投資，才能使總收益最大？最大總收益為多少？（注：收益與投入的單位都為“萬元”）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
