
| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
分析 利用a1a3-a${\;}_{2}^{2}$=1×2-12=1,a2a4-a${\;}_{3}^{2}$=1×3-22=-1,a3a5-a${\;}_{4}^{2}$=2×5-32=1,…,a2015a2017-a${\;}_{2016}^{2}$=1.即可得出.
解答 解:∵a1a3-a${\;}_{2}^{2}$=1×2-12=1,a2a4-a${\;}_{3}^{2}$=1×3-22=-1,
a3a5-a${\;}_{4}^{2}$=2×5-32=1,…,a2015a2017-a${\;}_{2016}^{2}$=1.
∴(a1a3-a${\;}_{2}^{2}$)(a2a4-a${\;}_{3}^{2}$)(a3a5-a${\;}_{4}^{2}$)…(a2015a2017-a${\;}_{2016}^{2}$)=11008×(-1)1007=-1.
故選:B.
點評 本題考查了斐波那契數列的性質及其應用,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若z是純虛數,則z2<0 | B. | 若z是虛數,則z2≥0 | ||
| C. | 若z2≥0,則z是實數 | D. | 若z2<0,則z是虛數 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 頻數 | 40 | 20 | a | 10 | b |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{3}{4}$,+∞) | B. | (-∞,$\frac{3}{4}$) | C. | (0,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
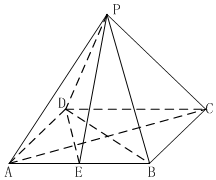 如圖,四棱錐P-ABCD的底面ABCD為矩形,AB=2$\sqrt{2}$,BC=2,點P在底面上的射影在AC上E是AB的中點.
如圖,四棱錐P-ABCD的底面ABCD為矩形,AB=2$\sqrt{2}$,BC=2,點P在底面上的射影在AC上E是AB的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com