
| A. | [-1,1] | B. | [-2,1] | C. | $[{-2,\sqrt{3}}]$ | D. | $[{-1,\sqrt{3}}]$ |
分析 化函數$f(x)=\sqrt{3}sinx-cosx$為正弦型函數,根據正弦函數的有界性和x的取值范圍求出f(x)的最值即可.
解答 解:函數$f(x)=\sqrt{3}sinx-cosx$
=2($\frac{\sqrt{3}}{2}$sinx-$\frac{1}{2}$cosx)
=2sin(x-$\frac{π}{6}$),
當$x∈[{-\frac{π}{2},\frac{π}{2}}]$時,-$\frac{2π}{3}$≤x-$\frac{π}{6}$≤$\frac{π}{3}$,
所以當x-$\frac{π}{6}$=-$\frac{π}{2}$,即x=-$\frac{π}{3}$時,
f(x)取得最小值為2×(-1)=-2;
當x-$\frac{π}{6}$=$\frac{π}{3}$,即x=$\frac{π}{2}$時,
f(x)取得最大值為2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$;
所以函數f(x)的值域為[-2,$\sqrt{3}$].
故選:C.
點評 本題考查了三角函數的圖象與性質的應用問題,是基礎題目.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
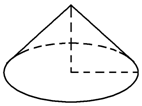 如圖,某養路處建造圓錐形倉庫用于貯藏食鹽(供融化高速公路上的積雪之用).已建的倉庫的底面直徑為12m,高4m,養路處擬建一個更大的圓錐形倉庫,以存放更多的食鹽,現有兩個方案:一是新建倉庫的底面直徑比原來的大4m(高不變),二是高度增加4m(底面直徑不變).
如圖,某養路處建造圓錐形倉庫用于貯藏食鹽(供融化高速公路上的積雪之用).已建的倉庫的底面直徑為12m,高4m,養路處擬建一個更大的圓錐形倉庫,以存放更多的食鹽,現有兩個方案:一是新建倉庫的底面直徑比原來的大4m(高不變),二是高度增加4m(底面直徑不變).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x>-2} | B. | {x|x<-2} | C. | {x|x>-1} | D. | {x|x≤-2} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 2016 | B. | 2017 | C. | log22016 | D. | log32016 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -12 | B. | -20 | C. | 12 | D. | 20 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com