已知函數(shù)f（x）=2sin（ωx+
）（ω＞0），x∈R．又f（x
1）=-2，f（x
2）=0且|x
1-x
2|的最小值等于π，則ω的值為
．
考點：正弦函數(shù)的圖象
專題：三角函數(shù)的圖像與性質(zhì)
分析：由|x1-x2|的最小值可得函數(shù)的周期值，進(jìn)而求出ω的大小．
解答：
解：∵f（x
1）=-2，f（x
2）=0且|x
1-x
2|的最小值等于π，
∴
=π，
即函數(shù)的周期T=4π，
∵T=
=4π，
解得ω=
，
故答案為：
點評：本題主要考查三角函數(shù)的圖象和性質(zhì)，根據(jù)函數(shù)最小值和零點之間的關(guān)系求出函數(shù)的周期是解決本題的關(guān)鍵．
練習(xí)冊系列答案
相關(guān)習(xí)題
科目：高中數(shù)學(xué)
來源：
題型：
如圖，在直徑為1的圓O中，作一關(guān)于圓心對稱、鄰邊互相垂直的十字形，其中y＞x＞0．
（1）將十字形的面積表示為θ的函數(shù)；
（2）十字形的最大面積是多少？并求出十字形取得最大值時，tanθ的值．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
對任意的a、b∈R，a≠b，且a+b=2，集合A={x|m＜x＜a2+b2}非空，則m的取值范圍是（ ）
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
如圖，正△ABC的邊長為2，P、Q分別在邊AB、AC上運動，且線段PQ將△ABC的面積二等分，求線段PQ長的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
在△ABC中，∠C=2∠A，a+c=10，cosA=
，求b．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知α，β∈（
，π），sin
+cos
=
，sin（α-β）=-
，則cosβ的值為（ ）
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
將4名新來的學(xué)生分到高三兩個班，每班至少一人，不同的分配方法數(shù)為（ ）
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
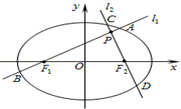
設(shè)橢圓E：
+=1（a＞b＞0）的長軸長為6，離心率e=
，O為坐標(biāo)原點．
（Ⅰ）求橢圓E標(biāo)準(zhǔn)方程；
（Ⅱ）設(shè)P（x
1，y
1），Q（x
2，y
2）是橢圓E上的兩點，
=(x1，y1)，=(x2，y2)，且
•=0，設(shè)M（x
0，y
0），且
=cosθ•+sinθ•（θ∈R），求x
02+3y
02的值；
（Ⅲ）如圖，若分別過橢圓E的左右焦點F
1，F(xiàn)
2的動直線?
1，?
2相交于P點，與橢圓分別交于A、B與C、D不同四點，直線OA、OB、OC、OD的斜率k
1、k
2、k
3、k
4滿足k
1+k
2=k
3+k
4．是否存在定點M、N，使得|PM|+|PN|為定值．若存在，求出M、N點坐標(biāo)；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
某縣共有300個村，按人均年可支配金額的多少分為三類，其中一類村有60個，二類村有100個．為了調(diào)查農(nóng)民的生活狀況，要抽出部分村作為樣本．現(xiàn)用分層抽樣的方法在一類村中抽出3個，則二類村、三類村共抽取的村數(shù)為
．
查看答案和解析>>
黃岡海淀全程培優(yōu)測試卷系列答案
