
分析 (1)利用等差數列的通項公式及前n項和公式表示出an與Sn,代入驗證即可確定出數列{an}的通項公式;
(2)令m=2,n=1確定出a1,a2,a3成等差數列,再利用數學歸納法證明對于一切n≥3的自然數,數列{an}是等差數列即可.
解答 解:(1)根據題意得:an=a1+(n-1)d,Sn=na1+$\frac{n(n-1)}{2}$d,
∴$\sqrt{{S}_{n}+n}$=$\sqrt{n({a}_{1}+\frac{n-1}{2}d+1)}$成等差數列,公差為d,
∴$\sqrt{{S}_{n}+n}$=dn,
∴$\left\{\begin{array}{l}{{a}_{1}+1-\fracp9vv5xb5{2}=0}\\{\sqrt{\fracp9vv5xb5{2}}=d}\end{array}\right.$,
解得:d=$\frac{1}{2}$,a1=-$\frac{3}{4}$,
則an=$\frac{1}{2}$n-$\frac{5}{4}$;
(2)令m=2,n=1,則$\frac{2{S}_{3}}{3}$=2a2,即$\frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}$=a2,
整理得:a1+a3=2a2,即a1,a2,a3成等差數列,
下面用數學歸納法證明{an}成等差數列,
假設a1,a2,…,ak成等差數列,其中k≥3,公差為d,
則令m=k,n=1,$\frac{2{S}_{k+1}}{k+1}$=ak+a1+d,
∴2Sk+1=(k+1)(ak+a1+d)=k(ak+a1)+a1+ak+(k+1)d=2Sk+a1+ak+(k+1)d,
∴2ak+1=a1+ak+(k+1)d=2(a1+kd),即ak+1=a1+kd,
∴a1,a2,…,ak,ak+1成等差數列,
則對于一切自然數,數列{an}是等差數列.
點評 此題考查了等差數列的性質,以及等差關系的確定,熟練掌握等差數列的性質是解本題的關鍵.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:選擇題
| A. | (0,+∞) | B. | (1,+∞) | C. | (e,+∞) | D. | $(\frac{e}{3},+∞)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
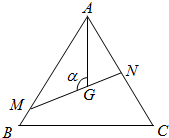 如圖,是△ABC邊長為1的正三角形,M,N分別是AB,AC邊上的點,線段MN過△ABC的重心,設∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.
如圖,是△ABC邊長為1的正三角形,M,N分別是AB,AC邊上的點,線段MN過△ABC的重心,設∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com