
【題目】某種產(chǎn)品的質(zhì)量以其質(zhì)量指標(biāo)值衡量,并依據(jù)質(zhì)量指標(biāo)值劃分等級如表:
質(zhì)量指標(biāo)值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等級 | 一等品 | 二等品 | 三等品 |
某企業(yè)從生產(chǎn)的這種產(chǎn)品中抽取100件產(chǎn)品作為樣本,檢測其質(zhì)量指標(biāo)值,得到下圖的率分布直方圖.(同一組數(shù)據(jù)用該區(qū)間的中點值作代表)
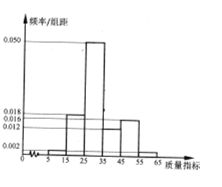
(1)該企業(yè)為提高產(chǎn)品質(zhì)量,開展了質(zhì)量提升月”活動,活動后再抽樣檢測,產(chǎn)品三等品數(shù)Y近似滿足Y~H(10,15,100),請測算“質(zhì)量提升月”活動后這種產(chǎn)品的“二等品率“(一、二等品其占全部產(chǎn)品百分比)較活動前提高多少個百分點?
(2)若企業(yè)每件一等品售價180元,每件二等品售價150元,每件三等品售價120元,以樣本中的頻率代替相應(yīng)概率,現(xiàn)有一名聯(lián)客隨機購買兩件產(chǎn)品,設(shè)其支付的費用為X(單位:元),求X的分布列及數(shù)學(xué)期望.
【答案】(1)5個百分點.(2)見解析,![]() .
.
【解析】
(1)根據(jù)抽樣調(diào)查數(shù)據(jù),求得樣本中一等品和二等品的件數(shù),得到在樣本中所占比例,再根據(jù)活動后產(chǎn)品三等品數(shù)Y近似滿足Y~H(10,15,100)得到一、二等品的合格率,兩個比例比較即可.
(2)根據(jù)樣品估計總體,該企業(yè)隨機抽取一件產(chǎn)品為一等品的概率為![]() ,二等品的概率為
,二等品的概率為![]() ,三等品的概率為
,三等品的概率為![]() ,再明確隨機變量X的所有可能取值為240,270,300,330,360,分別求得相應(yīng)概率,寫出分布列再求期望.
,再明確隨機變量X的所有可能取值為240,270,300,330,360,分別求得相應(yīng)概率,寫出分布列再求期望.
(1)根據(jù)抽樣調(diào)查數(shù)據(jù)知,樣本中一等品和二等品共有:(0.5+0.18+0.12)×100=80(件)
在樣本中所占比例為80%,
活動后產(chǎn)品三等品數(shù)Y近似滿足Y~H(10,15,100),
所以100件產(chǎn)品中三等品為15件,一、二等品數(shù)為100﹣15=85(件)合格率為85%,
所以一、二等品率增加了5個百分點.
(2)由樣品估計總體知,該企業(yè)隨機抽取一件產(chǎn)品為一等品的概率為![]() ,二等品的概率為
,二等品的概率為![]() ,三等品的概率為
,三等品的概率為![]() ,
,
隨機變量X的所有可能取值為240,270,300,330,360.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
所以X的分布列為:
X | 240 | 270 | 300 | 330 | 360 |
P(X) |
|
|
|
|
|
X的數(shù)學(xué)期望![]() .
.


 口算心算速算應(yīng)用題系列答案
口算心算速算應(yīng)用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于集合![]() ,
,![]() ,
,![]() ,
,![]() ,定義
,定義![]() .
.
集合![]() 中的元素個數(shù)記為
中的元素個數(shù)記為![]() ,當(dāng)
,當(dāng)![]() ,稱集合
,稱集合![]() 具有性質(zhì)
具有性質(zhì)![]() .
.
(1)已知集合![]() ,
,![]() ,寫出
,寫出![]() ,
,![]() 的值,并判斷集合
的值,并判斷集合![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() ;
;
(2)設(shè)集合![]() 具有性質(zhì)
具有性質(zhì)![]() ,判斷集合
,判斷集合![]() 中的三個元素是否能組成等差數(shù)列,請說明理由;
中的三個元素是否能組成等差數(shù)列,請說明理由;
(3)若數(shù)列![]() 是以
是以![]() 為首項,2為公比的等比數(shù)列. 數(shù)列
為首項,2為公比的等比數(shù)列. 數(shù)列![]() 中的前100項:
中的前100項:![]() 組成的集合
組成的集合![]() 記作
記作![]() ,將集合
,將集合![]() 中的所有元素
中的所有元素![]() 從小到大排序,即
從小到大排序,即![]() 滿足
滿足![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系中,以坐標(biāo)原點為極點,以![]() 軸正半軸為極軸,建立極坐標(biāo)系,點
軸正半軸為極軸,建立極坐標(biāo)系,點![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,直線
,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,且
,且![]() 過點
過點![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為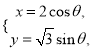 (
(![]() 為參數(shù)).
為參數(shù)).
(Ⅰ)求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值;
的距離的最大值;
(Ⅱ)過點![]() 與直線
與直線![]() 平行的直線
平行的直線![]() 與曲線
與曲線 ![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,現(xiàn)沿對角線
,現(xiàn)沿對角線![]() 將
將![]() 折起,使點A到達(dá)點P,點M,N分別在直線
折起,使點A到達(dá)點P,點M,N分別在直線![]() ,
,![]() 上,且A,B,M,N四點共面.
上,且A,B,M,N四點共面.
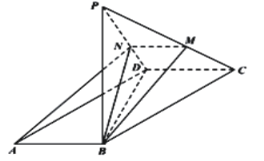
(1)求證:![]() ;
;
(2)若平面![]() 平面
平面![]() ,二面角
,二面角![]() 平面角大小為
平面角大小為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足![]() .
.
(1)求a1,a2,a3的值;
(2)對任意正整數(shù)n,an小數(shù)點后第一位數(shù)字是多少?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如城某觀光區(qū)的平面示意圖如圖所示,其中矩形![]() 的長
的長![]() 千米,寬
千米,寬![]() 千米,半圓的圓心
千米,半圓的圓心![]() 為
為![]() 中點.為了便于游客觀光休閑,在觀光區(qū)鋪設(shè)一條由圓弧
中點.為了便于游客觀光休閑,在觀光區(qū)鋪設(shè)一條由圓弧![]() 、線段
、線段![]() 、
、![]() 組成的觀光道路.其中線段
組成的觀光道路.其中線段![]() 經(jīng)過圓心
經(jīng)過圓心![]() ,且點
,且點![]() 在線段
在線段![]() 上(不含線段端點
上(不含線段端點![]() 、
、![]() ).已知道路
).已知道路![]() 、
、![]() 的造價為
的造價為![]() 元每千米,道路
元每千米,道路![]() 造價為
造價為![]() 元每千米,設(shè)
元每千米,設(shè)![]() ,觀光道路的總造價為
,觀光道路的總造價為![]() .
.
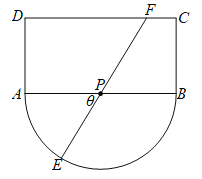
(1)試求![]() 與
與![]() 的函數(shù)關(guān)系式:
的函數(shù)關(guān)系式:![]() ;
;
(2)當(dāng)![]() 為何值時,觀光道路的總造價
為何值時,觀光道路的總造價![]() 最小.
最小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國古代儒家要求學(xué)生掌握六種基本才藝:禮、樂、射、御、書、數(shù),簡稱“六藝”,某高中學(xué)校為弘揚“六藝”的傳統(tǒng)文化,分別進(jìn)行了主題為“禮、樂、射、御、書、數(shù)”六場傳統(tǒng)文化知識競賽,現(xiàn)有甲、乙、丙三位選手進(jìn)入了前三名的最后角逐,規(guī)定:每場知識競賽前三名的得分都分別為![]()
![]() 且
且![]() ;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為
;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
A. 乙有四場比賽獲得第三名
B. 每場比賽第一名得分![]() 為
為![]()
C. 甲可能有一場比賽獲得第二名
D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)直線![]() 與直線
與直線![]() 分別與橢圓
分別與橢圓![]()
![]() 交于點
交于點![]() ,且四邊形
,且四邊形![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,是否存在經(jīng)過原點,且以
兩點,是否存在經(jīng)過原點,且以![]() 為直徑的圓?若有,請求出圓的方程,若沒有,請說明理由.
為直徑的圓?若有,請求出圓的方程,若沒有,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線C:x2=2py經(jīng)過點(2,1).
(Ⅰ)求拋物線C的方程及其準(zhǔn)線方程;
(Ⅱ)設(shè)O為原點,過拋物線C的焦點作斜率不為0的直線l交拋物線C于兩點M,N,直線y=1分別交直線OM,ON于點A和點B.求證:以AB為直徑的圓經(jīng)過y軸上的兩個定點.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com