
分析 (1)由題意可知:Sn=nan-n(n-1),當(dāng)n≥2時(shí),Sn-1=(n-1),an-1-(n-1)(n-2),由an=Sn-Sn-1,整理得:an-an-1=2,數(shù)列{an}是以1為首項(xiàng),2為公差的等差數(shù)列,由等差數(shù)列通項(xiàng)公式即可求得數(shù)列{an}的通項(xiàng)公式;
(2)由(1)可知:an=log3an-log3bn=log3$\frac{{a}_{n}}{{b}_{n}}$,求得$\frac{{a}_{n}}{{b}_{n}}$=${3}^{{a}_{n}}$,bn=$\frac{1}{3}$•(2n-1)•9n,利用“錯(cuò)位相減法”即可求得數(shù)列{bn}的前n項(xiàng)和Tn.
解答 解:(1)由題意可知:$\frac{S_n}{n}={a_n}-n+1$,Sn=nan-n(n-1),
當(dāng)n≥2時(shí),Sn-1=(n-1)an-1-(n-1)(n-2),
an=Sn-Sn-1=nan-n(n-1)-(n-1)an-1-(n-1)(n-2),
=nan-(n-1)an-1-2(n-1),
∴(n-1)an-(n-1)an-1=2(n-1),
∴an-an-1=2,
∴數(shù)列{an}是以1為首項(xiàng),2為公差的等差數(shù)列,
∴an=1+2(n-1)=2n-1,
數(shù)列{an}的通項(xiàng)公式an=2n-1;
(2)log3bn=log3an+an,
∴an=log3an-log3bn=log3$\frac{{a}_{n}}{{b}_{n}}$,
∴$\frac{{a}_{n}}{{b}_{n}}$=${3}^{{a}_{n}}$,
∴bn=an•${3}^{{a}_{n}}$=(2n-1)•32n-1=$\frac{1}{3}$•(2n-1)•9n,
∴數(shù)列{bn}的前n項(xiàng)和Tn,Tn=$\frac{1}{3}$[9+3×92+5×93+…+(2n-1)9n],
∴9Tn=$\frac{1}{3}$[92+3×93+5×94+…+(2n-3)9n+(2n-1)9n+1],
∴-8Tn=$\frac{1}{3}$[9+2(92+93+94+…+(9n)-(2n-1)9n+1],
=$\frac{1}{3}$[2×$\frac{9×(1-{9}^{n})}{9-1}$-9-(2n-1)•9n+1],
=$\frac{5-8n}{12}$×9n+1-$\frac{15}{4}$,
∴Tn=$\frac{8n-5}{96}$9n+1+$\frac{15}{32}$,
數(shù)列{bn}的前n項(xiàng)和Tn,Tn=$\frac{8n-5}{96}$9n+1+$\frac{15}{32}$.
點(diǎn)評(píng) 本題考查數(shù)列的遞推公式求數(shù)列的通項(xiàng)公式,考查等差數(shù)列的通項(xiàng)公式,“錯(cuò)位相減法”求數(shù)列的前n項(xiàng)和,考查計(jì)算能力,屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
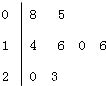 某品牌空調(diào)在4月1日至4月8日舉行促銷活動(dòng),如圖的莖葉圖表示某專賣店記錄的每天銷售量情況(單位:臺(tái)),則銷售量的中位數(shù)是15.
某品牌空調(diào)在4月1日至4月8日舉行促銷活動(dòng),如圖的莖葉圖表示某專賣店記錄的每天銷售量情況(單位:臺(tái)),則銷售量的中位數(shù)是15.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | ①②③④ | B. | ①③ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com