
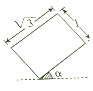
 一個放置在水平桌面上的正四棱柱的俯視圖如圖所示,其中α為銳角,則該幾何體的正視圖的面積的最大值為( )
一個放置在水平桌面上的正四棱柱的俯視圖如圖所示,其中α為銳角,則該幾何體的正視圖的面積的最大值為( )| A. | 2或3 | B. | 2$\sqrt{3}$或3 | C. | 1或3 | D. | 2或2$\sqrt{3}$ |
分析 根據正四棱柱的底面邊長是1還是$\sqrt{3}$,分兩種情況計算.
解答 解:由俯視圖可知正四棱柱的底面邊長為1,高為$\sqrt{3}$或底面邊長為$\sqrt{3}$,高為1,
由俯視圖可知主視圖矩形的一邊長為$\sqrt{3}$cosα+sinα=2sin(α+$\frac{π}{3}$),
(1)若正四棱柱的底面邊長為1,高為$\sqrt{3}$,
則正視圖的面積S=1•2sin(α+$\frac{π}{3}$)=2sin(α+$\frac{π}{3}$),
∴當α=$\frac{π}{6}$時,正視圖的面積最大,最大面積為2.
(2)若正四棱柱的底面邊長為$\sqrt{3}$,高為1,
則正視圖的面積S=$\sqrt{3}$•2sin(α+$\frac{π}{3}$)=2$\sqrt{3}$sin(α+$\frac{π}{3}$),
∴當α=$\frac{π}{6}$時,正視圖的面積最大,最大面積為2$\sqrt{3}$.
故選D.
點評 本題考查了棱柱的三視圖,屬于中檔題.


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\frac{14π}{6}+12$ | B. | $\frac{11π}{3}+4$ | C. | $\frac{11π}{6}+12$ | D. | $\frac{11π}{3}+12$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
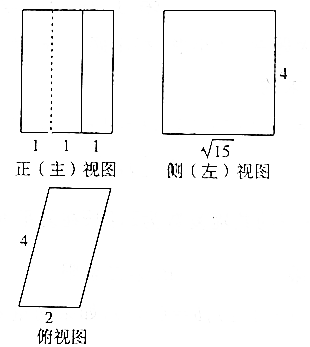 如圖,是一個幾何體的正視圖、側視圖、俯視圖,且正視圖、側視圖都是矩形,俯視圖是平行四邊形,則該幾何體的體積是( )
如圖,是一個幾何體的正視圖、側視圖、俯視圖,且正視圖、側視圖都是矩形,俯視圖是平行四邊形,則該幾何體的體積是( )| A. | $\frac{8\sqrt{15}}{3}$ | B. | 8$\sqrt{15}$ | C. | $\frac{4\sqrt{15}}{3}$ | D. | 4$\sqrt{15}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
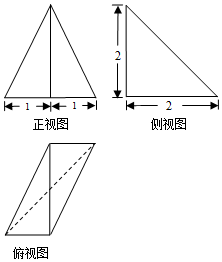 某三棱錐的三視圖如圖所示,則該三棱錐最長的棱長為( )
某三棱錐的三視圖如圖所示,則該三棱錐最長的棱長為( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 日期 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 優惠金額x(千元) | 10 | 11 | 13 | 12 | 8 |
| 銷售量y(輛) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 產品苜蓿草飼料 | A | B | C |
| 甲 | 4 | 8 | 3 |
| 乙 | 5 | 5 | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,1) | B. | [0,2] | C. | [-2,2) | D. | [-1,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com