
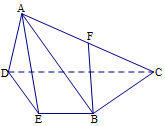
 如圖,在空間幾何體A-BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是邊長為2的等邊三角形,F為AC的中點.
如圖,在空間幾何體A-BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是邊長為2的等邊三角形,F為AC的中點.分析 (Ⅰ)取DA的中點G連結FG,GE,推導出四邊形BFGE為平行四邊形,從而BF∥EG,由此能證明BF∥平面ADE.
(Ⅱ)取DE的中點H,連AH,CH,推導出AH⊥DE,AH⊥HC,從而AH⊥平面BCDE,由此能證明平面ADE⊥BCDE.
(Ⅲ)幾何體C-BDF的體積${V_{C-BDF}}={V_{F-BDC}}=\frac{1}{2}{V_{A-BDC}}$,由此能求出結果.
解答 證明:(Ⅰ)取DA的中點G連結FG,GE,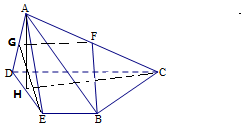 ∵F為AC的中點,∴$GF∥\frac{1}{2}DC,\;\;GF=\frac{1}{2}DC$,
∵F為AC的中點,∴$GF∥\frac{1}{2}DC,\;\;GF=\frac{1}{2}DC$,
又∵DC∥BE,CD=2BE,∴EB∥GF,且EB=GF,
∴四邊形BFGE為平行四邊形,∴BF∥EG,
∵EG?平面ADE,BF?平面ADE,
∴BF∥平面ADE…(4分)
解:(Ⅱ)取DE的中點H,連AH,CH,
∵△ADE為等邊三角形,∴AH⊥DE,且$AH=\sqrt{3}$,
在△DHC中,DH=1,DC=4,HDC=60°,∴$HC=\sqrt{13}$,
∴AC2=AH2+HC2,即AH⊥HC,∵DE∩HC=H,
∴AH⊥平面BCDE,∵AH?平面ADE,
∴平面ADE⊥BCDE…(8分)
(Ⅲ)${V_{A-BCD}}=\frac{1}{3}{S_{△BCD}}•AH$=$\frac{1}{3}×\frac{{4\sqrt{3}}}{2}×\sqrt{3}$=2,
∵F是AC中點,
∴幾何體C-BDF的體積${V_{C-BDF}}={V_{F-BDC}}=\frac{1}{2}{V_{A-BDC}}=1$.…(12分)
點評 本題考查線面平行、面面垂直的證明,考查幾何體的體積的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com