
分析 (1)分兩種情況進行研究,當0<x<80時,投入成本為C(x)=)$\frac{1}{3}{x}^{2}$+10x(萬元),根據年利潤=銷售收入-成本,列出函數關系式,當x≥80時,投入成本為C(x)=51x+$\frac{100000}{x}$-1450,根據年利潤=銷售收入-成本,列出函數關系式,最后寫成分段函數的形式,從而得到答案;
(2)根據年利潤的解析式,分段研究函數的最值,當0<x<80時,利用二次函數求最值,當x≥80時,利用基本不等式求最值,最后比較兩個最值,即可得到答案.
解答 解:(1)∵每件商品售價為0.05萬元,
∴x千件商品銷售額為0.05×1000x萬元,
①當0<x<80時,根據年利潤=銷售收入-成本,
∴L(x)=(0.05×1000x)-$\frac{1}{3}{x}^{2}$-10x-250=-$\frac{1}{3}{x}^{2}$+40x-250;
②當x≥80時,根據年利潤=銷售收入-成本,
∴L(x)=(0.05×1000x)-51x-$\frac{10000}{x}$+1450-250=1200-(x+$\frac{10000}{x}$).
綜合①②可得,L(x)=$\left\{\begin{array}{l}{-\frac{1}{3}{x}^{2}+40x-250,0<x<80}\\{1200-(x+\frac{10000}{x}),x≥80}\end{array}\right.$;
(2)①當0<x<80時,L(x)=-$\frac{1}{3}{x}^{2}$+40x-250=-$\frac{1}{3}(x-60)^{2}$+950,
∴當x=60時,L(x)取得最大值L(60)=950萬元;
②當x≥80時,L(x)=1200-(x+$\frac{10000}{x}$)≤1200-2$\sqrt{x•\frac{10000}{x}}$=1200-200=1000,
當且僅當x=$\frac{10000}{x}$,即x=100時,L(x)取得最大值L(100)=1000萬元.
綜合①②,由于950<1000,
∴年產量為100千件時,該廠在這一商品的生產中所獲利潤最大.
點評 考查學生根據實際問題選擇合適的函數類型的能力,以及運用基本不等式求最值的能力.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 26 | B. | 21 | C. | 18 | D. | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | 19 | C. | -1 | D. | -10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
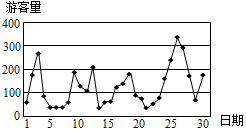 已知國家某5A級大型景區對擁擠等級與每日游客數量n(單位:百人)的關系有如下規定:當n∈[0,100)時,擁擠等級為“優”;當n∈[100,200)時,擁擠等級為“良”;當n∈[200,300)時,擁擠等級為“擁擠”;當n≥300時,擁擠等級為“嚴重擁擠”.該景區對6月份的游客數量作出如圖的統計數據:
已知國家某5A級大型景區對擁擠等級與每日游客數量n(單位:百人)的關系有如下規定:當n∈[0,100)時,擁擠等級為“優”;當n∈[100,200)時,擁擠等級為“良”;當n∈[200,300)時,擁擠等級為“擁擠”;當n≥300時,擁擠等級為“嚴重擁擠”.該景區對6月份的游客數量作出如圖的統計數據:| 游客數量 (單位:百人) | [0,100) | [100,200) | [200,300) | [300,400] |
| 天數 | a | 10 | 4 | 1 |
| 頻率 | b | $\frac{1}{3}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com