
【題目】關于![]() 的不等式
的不等式![]() ,對于
,對于![]() 恒成立,則實數
恒成立,則實數![]() 的取值范圍是________.
的取值范圍是________.
【答案】![]()
【解析】
設![]() ,則由
,則由![]() 得
得![]() ,則關于
,則關于![]() 的不等式
的不等式![]() 對任意
對任意![]() 恒成立等價于關于
恒成立等價于關于![]() 的不等式
的不等式![]() 對任意
對任意![]() 恒成立.分別討論當
恒成立.分別討論當![]() ,當
,當![]() 和當
和當![]() 的情況下一元二次不等式的恒成立問題,依次求出t的范圍最后再求并集即可.
的情況下一元二次不等式的恒成立問題,依次求出t的范圍最后再求并集即可.
設![]() ,則由
,則由![]() 得
得![]() ,
,
則關于![]() 的不等式
的不等式![]() 對任意
對任意![]() 恒成立等價于關于
恒成立等價于關于![]() 的不等式
的不等式![]() 對任意
對任意![]() 恒成立.
恒成立.
當![]() 時,不等式為
時,不等式為![]() ,即
,即![]() ①,
①,
令![]() ,要使①對任意
,要使①對任意![]() 恒成立,
恒成立,
則有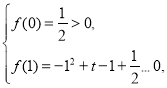 解得
解得![]() ;
;
當![]() 時,不等式為
時,不等式為![]() ,即
,即![]() ②,
②,
令![]() ,對稱軸
,對稱軸![]() ,且
,且![]() 開口向上,
開口向上,
則![]() 在
在![]() 上單調遞增,要使②對任意
上單調遞增,要使②對任意![]() 恒成立,
恒成立,
則有![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
當![]() 時,設
時,設![]() ,
,
易得當![]() 時,
時,![]() 取得最小值
取得最小值![]() ,
,
則由不等式![]() 對任意
對任意![]() 恒成立得
恒成立得![]() ,
,
所以![]() .
.
綜上所述,![]() 的取值范圍為
的取值范圍為![]() .
.
故答案為:![]()
【點晴】
本題考查不等式恒成立問題、二次函數的性質.含絕對值的不等式恒成立問題的常用解法:(1)對參數的取值范圍分類討論,去掉絕對值符號;(2)將不等式恒成立問題轉化為函數的最值問題求解.


科目:高中數學 來源: 題型:
【題目】已知點![]() 是橢圓
是橢圓![]() 上一動點,點
上一動點,點![]() 分別是左、右兩個焦點.
分別是左、右兩個焦點.![]() 面積的最大值為
面積的最大值為![]() ,且橢圓的長軸長為
,且橢圓的長軸長為![]() .
.
(1)求橢圓的標準方程;
(2)若點![]() ,
,![]() 在橢圓上,已知兩點
在橢圓上,已知兩點![]() ,
,![]() ,且以
,且以![]() 為直徑的圓經過坐標原點
為直徑的圓經過坐標原點![]() .求證:
.求證:![]() 的面積
的面積![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點,
的中點,![]() ,將
,將![]() 沿
沿![]() 折起,得到四棱錐
折起,得到四棱錐![]() ,
,![]() 為
為![]() 的中點.
的中點.
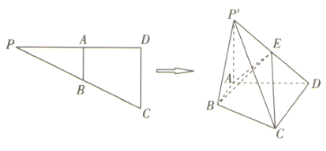
(1)證明:![]() 平面
平面![]() ;
;
(2)當正視圖方向與向量![]() 的方向相同時,
的方向相同時,![]() 的正視圖為直角三角形,求此時二面角
的正視圖為直角三角形,求此時二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為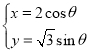 (
(![]() 為參數),若以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線
為參數),若以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點P的坐標為![]() ,且曲線
,且曲線![]() 與曲線
與曲線![]() 交于C,D兩點,求
交于C,D兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點,
的中點,![]() ,將
,將![]() 沿
沿![]() 折起,得到四棱錐
折起,得到四棱錐![]() ,
,![]() 為
為![]() 的中點.
的中點.
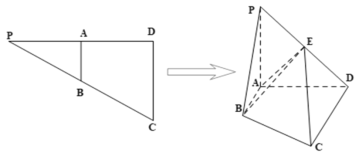
(1)證明:![]() 平面
平面![]() ;
;
(2)當正視圖方向與向量![]() 的方向相同時,此時
的方向相同時,此時![]() 的正視圖的面積為
的正視圖的面積為![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ;數列
;數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,
, ![]() ,
, ![]() .
.
(1)求數列![]() 、
、![]() 的通項公式;
的通項公式;
(2)是否存在正整數![]() ,使得
,使得![]() 恰為數列
恰為數列![]() 中的一項?若存在,求所有滿足要求的
中的一項?若存在,求所有滿足要求的![]() ;若不存在,說明理由.
;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
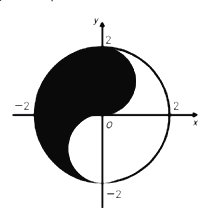
【題目】眾所周知的“太極圖”,其形狀如對稱的陰陽兩魚互抱在一起,也被稱為“陰陽魚太極圖”.如圖是放在平面直角坐標系中的“太極圖”.整個圖形是一個圓形.其中黑色陰影區域在y軸右側部分的邊界為一個半圓,給出以下命題:
①在太極圖中隨機取一點,此點取自黑色陰影部分的概率是![]()
②當![]() 時,直線y=ax+2a與白色部分有公共點;
時,直線y=ax+2a與白色部分有公共點;
③黑色陰影部分(包括黑白交界處)中一點(x,y),則x+y的最大值為2;
④設點P(﹣2,b),點Q在此太極圖上,使得∠OPQ=45°,b的范圍是[﹣2,2].
其中所有正確結論的序號是( )
A.①④B.①③C.②④D.①②
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com