
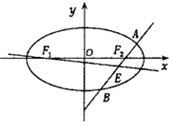
 已知橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一條漸近線與x軸所成的夾角為30°,且雙曲線的焦距為4$\sqrt{2}$.
已知橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一條漸近線與x軸所成的夾角為30°,且雙曲線的焦距為4$\sqrt{2}$.分析 (1)由雙曲線的漸近線方程及斜率公式,即可求得a2=3b2,c=2$\sqrt{2}$,即a2+b2=8,即可求得a和b的值,求得橢圓方程;
(2)設直線AB的方程,代入橢圓方程,利用韋達定理求得斜率丨k丨用t表示,利用基本不等式即可求得k的取值范圍.
解答 解:(1)由一條漸近線與x軸所成的夾角為30°,則$\frac{b}{a}$=tan30°=$\frac{\sqrt{3}}{3}$,即a2=3b2,
由2c=4$\sqrt{2}$.c=2$\sqrt{2}$,則a2+b2=8,
解得:a2=8,b2=2,
∴橢圓的標準方程:$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$;
(2)由(1)可知:F2(2,0),直線AB的方程:x=ty+2,A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}{x=ty+2}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,整理得:(t2+3)y2+4ty-2=0,
y1+y2=-$\frac{4t}{{t}^{2}+3}$,x1+x2=$\frac{12}{{t}^{2}+3}$,
則E($\frac{6}{{t}^{2}+3}$,-$\frac{2t}{{t}^{2}+3}$),
由F1(-2,0),則直線F1E的斜率k=$\frac{\frac{2t}{{t}^{2}+3}}{-2-\frac{6}{{t}^{2}+3}}$=-$\frac{t}{{t}^{2}+6}$,
①當t=0時,k=0,
②當t≠0時,丨k丨=$\frac{丨t丨}{丨t{丨}^{2}+6}$=$\frac{1}{丨t丨+\frac{6}{丨t丨}}$≤$\frac{1}{2\sqrt{6}}$,
即丨k丨∈(0,$\frac{\sqrt{6}}{12}$],
∴k的取值范圍[-$\frac{\sqrt{6}}{12}$,$\frac{\sqrt{6}}{12}$].
點評 本題考查橢圓的標準方程,直線與橢圓的位置關系,考查韋達定理,直線的斜率公式及基本不等式的應用,考查計算能力,屬于中檔題.


 作業輔導系列答案
作業輔導系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
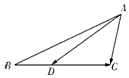 如圖,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC邊上一點,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,則$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值為-2.
如圖,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC邊上一點,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,則$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值為-2.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
| 單價x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 銷量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com