
分析 (Ⅰ)利用三角恒等變換化簡f(x)的解析式,再利用正弦函數的圖象的對稱性,求得函數f(x)的對稱軸方程.
(Ⅱ)利用函數y=Asin(ωx+φ)的圖象變換規律求得g(x)的解析式,再利用余弦定理求得b的值.
解答 解:(Ⅰ)函數$f(x)=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}$=$\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}(1+cos2x)-\frac{1}{2}=sin(2x-\frac{π}{6})-1$,
令$2x-\frac{π}{6}=kπ+\frac{π}{2},k∈Z$,解得$x=\frac{kπ}{2}+\frac{π}{3},k∈Z$,
所以函數f(x)的對稱軸方程為$x=\frac{kπ}{2}+\frac{π}{3},k∈Z$.
(Ⅱ)函數f(x)的圖象各點縱坐標不變,橫坐標伸長為原來的2倍,得到函數$y=sin(x-\frac{π}{6})-1$的圖象,
再向左平移$\frac{π}{3}$個單位,得到函數$y=sin(x+\frac{π}{3}-\frac{π}{6})-1$的圖象,所以函數$g(x)=sin(x+\frac{π}{6})-1$.
又△ABC中,g(B)=0,所以$sin(B+\frac{π}{6})-1=0$,又$\frac{π}{6}<B+\frac{π}{6}<\frac{7π}{6}$,
所以$B+\frac{π}{6}=\frac{π}{2}$,則$B=\frac{π}{3}$.由余弦定理可知,${b^2}={a^2}+{c^2}-2accosB={2^2}+{4^2}-2×2×4cos\frac{π}{3}=12$,
所以$b=2\sqrt{3}$.
點評 本題主要考查三角恒等變換,正弦函數的圖象的對稱性,函數y=Asin(ωx+φ)的圖象變換規律,余弦定理,屬于中檔題.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:解答題
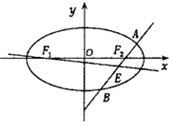 已知橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一條漸近線與x軸所成的夾角為30°,且雙曲線的焦距為4$\sqrt{2}$.
已知橢圓C的方程為$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一條漸近線與x軸所成的夾角為30°,且雙曲線的焦距為4$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,4) | B. | (4,-2) | C. | (-4,6) | D. | (4,6] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com