
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.直線
軸正半軸為極軸建立極坐標系.直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程與直線
的極坐標方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,求
,求![]() .
.
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() ,且與定直線
,且與定直線![]() 相切.
相切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的任一條直線
的任一條直線![]() 與軌跡
與軌跡![]() 交于不同的兩點
交于不同的兩點![]() ,試探究在
,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() (異于點
(異于點![]() ),使得
),使得![]() ?若存在,求點
?若存在,求點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:![]() ,直線1過原點O.
,直線1過原點O.
(1)若直線l與圓C相切,求直線l的斜率;
(2)若直線l與圓C交于A、B兩點,點P的坐標為![]() ,若
,若![]() .求直線l的方程.
.求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠去年某產品的年產量為100萬只,每只產品的銷售價為10元,固定成本為8元![]() 今年,工廠第一次投入100萬元
今年,工廠第一次投入100萬元![]() 科技成本
科技成本![]() ,并計劃以后每年比上一年多投入100萬元
,并計劃以后每年比上一年多投入100萬元![]() 科技成本
科技成本![]() ,預計產量年遞增10萬只,第
,預計產量年遞增10萬只,第![]() 次投入后,每只產品的固定成本為
次投入后,每只產品的固定成本為![]() 為常數,
為常數,![]() 且
且![]() ,若產品銷售價保持不變,第
,若產品銷售價保持不變,第![]() 次投入后的年利潤為
次投入后的年利潤為![]() 萬元.
萬元.
(1)求![]() 的值,并求出
的值,并求出![]() 的表達式;
的表達式;
(2)問從今年算起第幾年利潤最高?最高利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確的是
(1)命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l為直線,![]() ,
,![]() 為兩個不同的平面,若
為兩個不同的平面,若![]() ,
,![]() ,則
,則![]() ;
;
(3)給定命題p,q,若“![]() 為真命題”,則
為真命題”,則![]() 是假命題;
是假命題;
(4)“![]() ”是“
”是“![]() ”的充分不必要條件.
”的充分不必要條件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為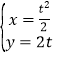 (t為參數),曲線C2的參數方程為
(t為參數),曲線C2的參數方程為![]() (α為參數),以O為極點,x軸的正半軸為極軸建立極坐標系.
(α為參數),以O為極點,x軸的正半軸為極軸建立極坐標系.
(1)求曲線C1和C2的極坐標方程;
(2)直線l的極坐標方程為![]() ,直線l與曲線C1和C2分別交于不同于原點的A,B兩點,求|AB|的值.
,直線l與曲線C1和C2分別交于不同于原點的A,B兩點,求|AB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一列非零向量![]() 滿足:
滿足:![]() (其中
(其中![]() 是非零常數).
是非零常數).
(1)求數列![]() 的通項公式;
的通項公式;
(2)求向量![]() 與
與![]() 夾角
夾角![]() 的弧度數
的弧度數![]()
(3)當![]() 時,把
時,把![]() 中所有與
中所有與![]() 共線的向量按原來的順序排成一列,記為
共線的向量按原來的順序排成一列,記為![]() 令
令![]()
![]() 為坐標原點,求點列
為坐標原點,求點列![]() 的極限點D的坐標.(注:若點
的極限點D的坐標.(注:若點![]() 坐標為
坐標為![]() 且
且![]() 則稱點D
則稱點D![]() 為點列
為點列![]() 的極限點).
的極限點).
查看答案和解析>>
科目:高中數學 來源: 題型:
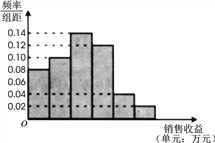
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入![]() 萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從
萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從![]() 開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司投入![]() 萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 7 |
由表中的數據顯示, ![]() 與
與![]() 之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出
之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出![]() 關于
關于![]() 的回歸直線方程.
的回歸直線方程.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com