
分析 (1)先求出圓心坐標,可得圓的方程,再設出切線方程,利用點到直線的距離公式,即可求得切線方程;
(2)設出點C,M的坐標,利用|MA|=2|MO|,尋找坐標之間的關系,進一步將問題轉化為圓與圓的位置關系,即可得出結論.
解答 解:(1)由題設,圓心C在y=x-3上,也在直線y=2x-4上,2a-4=a-3,∴a=1,∴C(1,-2).
∴⊙C:(x-1)2+(y+2)2=1,
由題,當斜率存在時,過A點切線方程可設為y=kx+3,即kx-y+3=0,則$\frac{|k+5|}{\sqrt{1+{k}^{2}}}$=1,解得:k=-$\frac{12}{5}$,…(4分)
又當斜率不存在時,也與圓相切,∴所求切線為x=0或y=-$\frac{12}{5}$x+3,
即x=0或12x+5y-15=0;
(2)設點M(x,y),由|MA|=2|MO|,化簡得:x2+(y+1)2=4,
∴點M的軌跡為以(0,-1)為圓心,2為半徑的圓,可記為圓D,
又∵點M在圓C上,
∴圓C與圓D的關系為相交或相切,
∴1≤|CD|≤3,其中|CD|=$\sqrt{{a}^{2}+(2a-3)^{2}}$,
∴1≤$\sqrt{{a}^{2}+(2a-3)^{2}}$≤3,
解得:0≤a≤$\frac{12}{5}$.
點評 此題考查了圓的切線方程,點到直線的距離公式,以及圓與圓的位置關系的判定,涉及的知識有:兩直線的交點坐標,直線的點斜式方程,兩點間的距離公式,圓的標準方程,是一道綜合性較強的試題.


科目:高中數學 來源: 題型:選擇題
| A. | 1或2 | B. | 2 | C. | 1 | D. | 1或-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
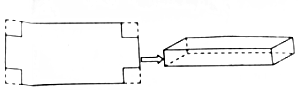 如圖,在一張長為2a米,寬為a米(a>2)的矩形鐵皮的四個角上,各剪去一個邊長是x米(0<x≤1)的小正方形,折成一個無蓋的長方體鐵盒,設V(x)表示鐵盒的容積.
如圖,在一張長為2a米,寬為a米(a>2)的矩形鐵皮的四個角上,各剪去一個邊長是x米(0<x≤1)的小正方形,折成一個無蓋的長方體鐵盒,設V(x)表示鐵盒的容積.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示的多面體中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.
如圖所示的多面體中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{1}{6}$,$\frac{1}{3}$) | B. | [$\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{3}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com