【題目】已知 
．
（1）若函數
的值域為
，求實數
的取值范圍；
（2）若函數
在區間
上是減函數，求實數
的取值范圍．
【答案】（1）
或
；（2）
.
【解析】試題分析：（1）函數
的值域為
，即是不等式
的解集為
，利用二次函數性質可得判別式小于零即可得結果；（2）根據區間
即是函數
定義域的子集又是二次函數減區間的子集，列不等式組求解即可.
試題解析：（1）f（x）值域為R，令g（x）=x2﹣mx﹣m， 則g（x）取遍所有的正數
即△=m2+4m≥0
∴m≥0或m≤﹣4；
（2）由題意知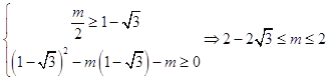 
.
【方法點晴】本題主要考查函數的定義域、值域及利用單調性求參數的范圍，屬于中檔題. 利用單調性求參數的范圍的常見方法：① 視參數為已知數，依據函數的圖象或單調性定義，確定函數的單調區間，與已知單調區間比較求參數需注意若函數在區間
上是單調的，則該函數在此區間的任意子集上也是單調的; ② 利用導數轉化為不等式
或
恒成立問題求參數范圍，本題（2）是利用方法 ① 求解的．
科目：高中數學 來源： 題型：
【題目】某市某水產養殖戶進行小龍蝦銷售，已知每千克小龍蝦養殖成本為6元，在整個銷售旺季的80天里，銷售單價
（元/千克）與時間第
（天）之間的函數關系為：
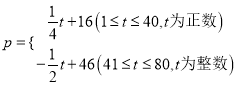，日銷售量
（千克）與時間第
（天）之間的函數關系如圖所示：
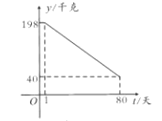
（1）求日銷售量
與時間
的函數關系式？
（2）哪一天的日銷售利潤最大？最大利潤是多少？
（3）在實際銷售的前40天中，該養殖戶決定每銷售1千克小龍蝦，就捐贈
元給村里的特困戶，在這前40天中，每天扣除捐贈后的日銷售利潤隨時間
的增大而增大，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】拋物線C:y2＝2px(p＞0)的準線為l，焦點為F．⊙M的圓心在x軸的正半軸上，且與y軸相切．過原點O作傾斜角為
的直線n交l于點A， 交⊙M于另一點B，且AO＝OB＝2．
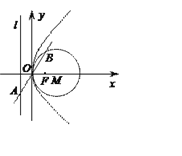
(1)求⊙M和拋物線C的方程；
(2)若P為拋物線C上的動點，求
的最小值；
(3)過l上的動點Q向⊙M作切線，切點為S，T，求證：直線ST恒過一個定點，并求該定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-5：不等式選講
已知函數f（x）=|2x＋1|+|2x－a|．
（I）若f（x）的最小值為2，求a的值；
（II）若f（x）≤|2x－4|的解集包含[－2，－1]，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-5：不等式選講
已知函數f（x）=|2x＋1|+|2x－a|．
（I）若f（x）的最小值為2，求a的值；
（II）若f（x）≤|2x－4|的解集包含[－2，－1]，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=lg（ax﹣bx），且f（1）=lg2，f（2）=lg12
（1）求a，b的值．
（2）當x∈[1，2]時，求f（x）的最大值．
（3）m為何值時，函數g（x）=ax的圖象與h（x）=bx﹣m的圖象恒有兩個交點．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
