
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入
(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入![]() (萬元)滿足
(萬元)滿足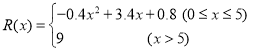 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,完成下列問題:
(1)寫出利潤函數![]() 的解析式(利潤=銷售收入-總成本);
的解析式(利潤=銷售收入-總成本);
(2)甲廠生產多少臺產品時,可使盈利最多?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】為振興旅游業,香港計劃向內陸地區發行總量為2000萬張的紫荊卡,其中向內陸人士(廣東戶籍除外)發行的是紫荊金卡(簡稱金卡),向廣東籍人士發行的是紫荊銀卡(簡稱銀卡).某旅游公司組織了一個有36名內陸游客的旅游團到香港名勝旅游,其中![]() 是非廣東籍內陸游客,其余是廣東籍游客.在非廣東新游客中有
是非廣東籍內陸游客,其余是廣東籍游客.在非廣東新游客中有![]() 持金卡,在廣東籍游客中有
持金卡,在廣東籍游客中有![]() 持銀卡.
持銀卡.
(Ⅰ)在該團中隨機采訪3名游客,求恰有1人持金卡且持銀卡者少于2人的概率;
(Ⅱ)在該團的廣東籍游客中隨機采訪3名游客,設其中持銀卡人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數![]() ,定義域為
,定義域為![]() 的函數
的函數![]() 是偶函數,其中
是偶函數,其中![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)求實數![]() 值;
值;
(Ⅱ)判斷該函數![]() 在
在![]() 上的單調性并用定義證明;
上的單調性并用定義證明;
(Ⅲ)是否存在實數![]() ,使得對任意的
,使得對任意的![]() ,不等式
,不等式![]() 恒成立.若存在,求出實數
恒成立.若存在,求出實數![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了確定下一年度投入某種產品的宣傳費用,需了解年宣傳費x(單位:萬元)對年銷量y(單位:噸)和年利潤(單位:萬元)的影響.對近6宣傳費xi和年銷售量yi(i=1,2,3,4,5,6)的數據做了初步統計,得到如下數據:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣傳費x(萬元) | 38 | 48 | 58 | 68 | 78 | 88 |
年銷售量y(噸) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
經電腦模擬,發現年宣傳費x(萬元)與年銷售量y(噸)之間近似滿足關系式y=axb(a,b>0),即lny=blnx+lna.,對上述數據作了初步處理,得到相關的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)從表中所給出的6年年銷售量數據中任選2年做年銷售量的調研,求所選數據中至多有一年年銷售量低于20噸的概率.
(Ⅱ)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅲ) 若生產該產品的固定成本為200(萬元),且每生產1(噸)產品的生產成本為20(萬元)(總成本=固定成本+生產成本+年宣傳費),銷售收入為![]() (萬元),假定該產品產銷平衡(即生產的產品都能賣掉),則2019年該公司應該投入多少宣傳費才能使利潤最大?(其中
(萬元),假定該產品產銷平衡(即生產的產品都能賣掉),則2019年該公司應該投入多少宣傳費才能使利潤最大?(其中![]() )
)
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為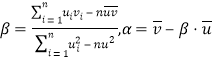
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() ,其右焦點為
,其右焦點為![]() .點
.點![]() 是橢圓
是橢圓![]() 上異于長軸端點的任意一點,連接
上異于長軸端點的任意一點,連接![]() 并延長交橢圓
并延長交橢圓![]() 于點
于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且直線
為坐標原點,且直線![]() 與右準線
與右準線![]() 交于點
交于點![]() .
.
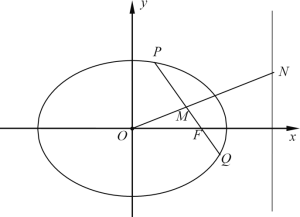
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
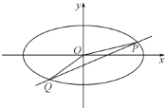
(Ⅰ)求橢圓方程;
(Ⅱ)設不過原點![]() 的直線
的直線![]() ,與該橢圓交于
,與該橢圓交于![]() 兩點,直線
兩點,直線![]() 的斜率分別為
的斜率分別為![]() ,滿足
,滿足![]() .
.
(i)當![]() 變化時,
變化時,![]() 是否為定值?若是,求出此定值,并證明你的結論;若不是,請說明理由;
是否為定值?若是,求出此定值,并證明你的結論;若不是,請說明理由;
(ii)求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,過點
,過點![]() 做
做![]() 軸的垂線交橢圓于
軸的垂線交橢圓于![]() 兩點,且
兩點,且![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 為橢圓
為橢圓![]() 短軸的上頂點,直線
短軸的上頂點,直線![]() 不經過
不經過![]() 點且與
點且與![]() 相交于
相交于![]() 兩點,若直線
兩點,若直線![]() 與直線
與直線![]() 的斜率的和為
的斜率的和為![]() ,問:直線
,問:直線![]() 是否過定點?若是,求出這個定點,否則說明理由.
是否過定點?若是,求出這個定點,否則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com