【題目】已知三棱錐
如圖所示，其中
， 
，二面角
的大小為
.
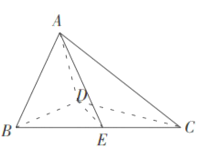
（1）證明： 
；
（2）若
為線段
的中點，且
， 
，求二面角
的余弦值.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體是圓柱的一部分，它是由矩形
（及其內部）以
邊所在直線為旋轉軸旋轉
得到的，點
是弧
上的一點，點
是弧
的中點.
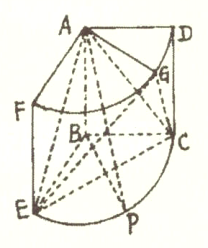
（1）求證：平面
平面
；
（2）當
且
時，求二面角
的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律：每生產產品
（百臺），其總成本為
（萬元），其中固定成本為2.8萬元，并且每生產1百臺的生產成本為1萬元（總成本=固定成本+生產成本），銷售收入
（萬元）滿足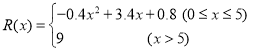
，假定該產品產銷平衡（即生產的產品都能賣掉），根據上述統計規律，完成下列問題：
（1）寫出利潤函數
的解析式（利潤=銷售收入－總成本）；
（2）甲廠生產多少臺產品時，可使盈利最多？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為
，直線
與拋物線
交于
兩點．
（Ⅰ）若直線
過焦點
，且與圓
交于
（其中
在
軸同側），求證： 
是定值；
（Ⅱ）設拋物線
在
和
點的切線交于點
，試問： 
軸上是否存在點
，使得
為菱形？若存在，請說明理由并求此時直線
的斜率和點
的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f(x)＝
，x∈(－2，2)．
(1) 判斷f(x)的奇偶性并說明理由；
(2) 求證：函數f(x)在(－2，2)上是增函數；
(3) 若f(2＋a)＋f(1－2a)>0，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高校數學與統計學院為了對2018年錄取的大一新生有針對性地進行教學.從大一新生中隨機抽取40名，對他們在2018年高考的數學成績進行調查，統計發現40名新生的數學分數
分布在
內.當
時，其頻率
.
（Ⅰ）求
的值；
（Ⅱ）請在答題卡中畫出這40名新生高考數學分數的頻率分布直方圖，并估計這40名新生的高考數學分數的平均數；
（Ⅲ）從成績在100～120分的學生中，用分層抽樣的方法從中抽取5名學生，再從這5名學生中隨機選兩人甲、乙，記甲、乙的成績分別為
，求概率
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝1－
(a>0，a≠1)且f(0)＝0.
(1)求a的值；
(2)若函數g(x)＝(2x＋1)·f(x)＋k有零點，求實數k的取值范圍；
(3)當x∈(0，1)時，f(x)>m·2x－2恒成立，求實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
