
【題目】為振興旅游業,香港計劃向內陸地區發行總量為2000萬張的紫荊卡,其中向內陸人士(廣東戶籍除外)發行的是紫荊金卡(簡稱金卡),向廣東籍人士發行的是紫荊銀卡(簡稱銀卡).某旅游公司組織了一個有36名內陸游客的旅游團到香港名勝旅游,其中![]() 是非廣東籍內陸游客,其余是廣東籍游客.在非廣東新游客中有
是非廣東籍內陸游客,其余是廣東籍游客.在非廣東新游客中有![]() 持金卡,在廣東籍游客中有
持金卡,在廣東籍游客中有![]() 持銀卡.
持銀卡.
(Ⅰ)在該團中隨機采訪3名游客,求恰有1人持金卡且持銀卡者少于2人的概率;
(Ⅱ)在該團的廣東籍游客中隨機采訪3名游客,設其中持銀卡人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】試題分析:(Ⅰ)由題意得,境外游客有27人,其中9人持金卡;境內游客有9人,其中6人持銀卡.記出事件,表示出事件的概率,根據互斥事件的概率公式,得到結論;(Ⅱ)ξ的可能取值為0,1,2,3,分別求出其對應的概率,能得到ξ的分布列和數學期望Eξ.
解析:
(Ⅰ)由題意得,非廣東籍游客有27人,其中9人持金卡:廣東籍游客有9人,其中6人持銀卡,設事件![]() 為“采訪該團3人中,恰有1人持金卡且持銀卡者少于2人”,
為“采訪該團3人中,恰有1人持金卡且持銀卡者少于2人”,
事件![]() 為“采訪該團3人中,1人持金卡,0人持銀卡”,
為“采訪該團3人中,1人持金卡,0人持銀卡”,
事件![]() 為“采訪該團3人中,1人持金卡,1人持銀卡”.
為“采訪該團3人中,1人持金卡,1人持銀卡”.
![]() ,
,
所以在該團中隨機來訪3人,恰有1人持金卡且持銀卡者少于2人的概率是![]() .
.
(Ⅱ)![]() 的可能取值為0,1,2,3.
的可能取值為0,1,2,3.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率為80%.現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4,5,6,7,8表示命中,9,0表示未命中;再以每三個隨機數為一組,代表三次投籃的結果.經隨機模擬產生了如下20組隨機數:
907 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
據此估計,該運動員三次投籃均命中的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自出生之日起,人的情緒、體力、智力等心理、生理狀況就呈周期變化,變化由線為![]() .根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
.根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
(1)請寫出小英的體力、情緒和智力節律曲線的函數;
(2)試判斷小英在2019年4月22日三種節律各處于什么階段,當日小英是否適合參加某項體育競技比賽?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生對某小區30位居民的飲食習慣進行了一次調查,并用如圖所示的莖葉圖表示他們的飲食指數(說明:圖中飲食指數低于70的人,飲食以蔬菜為主;飲食指數高于70的,飲食以肉類為主).

(1)根據莖葉圖,說明這30位居民中50歲以上的人的飲食習慣;
(2)根據以上數據完成如下2×2列聯表;
主食蔬菜 | 主食肉類 | 總計 | |
50歲以下 | |||
50歲以上 | |||
總計 |
(3)能否有99%的把握認為居民的飲食習慣與年齡有關?
獨立性檢驗的臨界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市為了制定合理的節水方案,對居民用水情況進行調查,通過抽樣,獲得某年100為居民每人的月均用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
(1)求直方圖的![]() 的值;
的值;
(2)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,說明理由.
(3)估計居民月用水量的中位數.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】墻上有一壁畫,最高點![]() 處離地面
處離地面![]() 米,最低點
米,最低點![]() 處離地面
處離地面![]() 米,距離墻
米,距離墻![]() 米處設有防護欄,觀察者從離地面高
米處設有防護欄,觀察者從離地面高![]() 米的
米的![]() 處觀賞它.
處觀賞它.
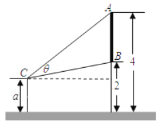
(1)當![]() 時,觀察者離墻多遠時,視角
時,觀察者離墻多遠時,視角![]() 最大?
最大?
(2)若![]() ,視角
,視角![]() 的正切值恒為
的正切值恒為![]() ,觀察者離墻的距離應在什么范圍內?
,觀察者離墻的距離應在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品![]() (百臺),其總成本為
(百臺),其總成本為![]() (萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入
(萬元),其中固定成本為2.8萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入![]() (萬元)滿足
(萬元)滿足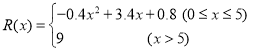 ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,完成下列問題:
(1)寫出利潤函數![]() 的解析式(利潤=銷售收入-總成本);
的解析式(利潤=銷售收入-總成本);
(2)甲廠生產多少臺產品時,可使盈利最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com