
分析 (1)從9個自然數中,任取3個不同的數,共有${C}_{9}^{3}$=84種等可能的結果,由條件得最大的在中間,其它兩個排兩邊,有2種排法,由此能求出這樣的三位數的個數.
(2)由題意得X的取值范圍為0,1,2,3,分別求出相應的概率,由此能求出隨機變量X的分布列和數學期望.
解答 解:(1)從9個自然數中,任取3個不同的數,共有${C}_{9}^{3}$=84種等可能的結果…(2分)
由條件得最大的在中間,其它兩個排兩邊,有2種排法,…(4分)
所以這樣的三位數共有$C_9^3×2=84×2=168$個.…(6分)
(2)由題意得X的取值范圍為0,1,2,3,…(7分)
P(X=0)=$\frac{C_5^0C_4^3}{C_9^3}=\frac{1}{21}$,P(X=1)=,
P(X=2)=$\frac{C_5^2C_4^1}{C_9^3}=\frac{10}{21}$,P(X=3)=$\frac{C_5^3C_4^0}{C_9^3}=\frac{5}{42}$,
∴隨機變量X的分布列為:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{21}$ | $\frac{5}{14}$ | $\frac{10}{21}$ | $\frac{5}{42}$ |
點評 本題考查排列組合數的求法,考查離散型隨機變量的分布列和數學期望的求法,是中檔題,解題時要認真審題,注意等可能事件概率計算公式的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
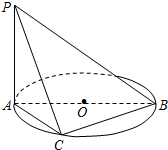 已知PA垂直于以AB為直徑的ΘO所在的平面,C是ΘO上異于A,B的動點,PA=1,AB=2,當三棱錐P-ABC取得最大體積時,求:
已知PA垂直于以AB為直徑的ΘO所在的平面,C是ΘO上異于A,B的動點,PA=1,AB=2,當三棱錐P-ABC取得最大體積時,求:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知在四棱錐P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分別是線段AB、BC的中點.
已知在四棱錐P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分別是線段AB、BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com