
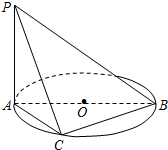
 已知PA垂直于以AB為直徑的ΘO所在的平面,C是ΘO上異于A,B的動點,PA=1,AB=2,當三棱錐P-ABC取得最大體積時,求:
已知PA垂直于以AB為直徑的ΘO所在的平面,C是ΘO上異于A,B的動點,PA=1,AB=2,當三棱錐P-ABC取得最大體積時,求:分析 (1)由題意可知,△ACB為等腰直角三角形,補形后求解直角三角形可得PC與AB所成角的大小;
(2)由PA⊥平面ABC,得PA⊥BC,又BC⊥AC,可得BC⊥平面PAC,則平面PBC⊥平面PAC,過A作AT⊥PC,垂足為T,則AT⊥平面PBC,∠APT即為PA與平面PCB所成角,然后求解直角三角形可得PA與面PCB所成角的大小.
解答 解:(1)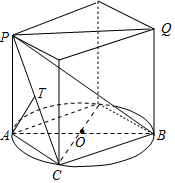 如圖,三棱錐P-ABC高PA=1,要使體積最大,則底面△ABC的面積最大,
如圖,三棱錐P-ABC高PA=1,要使體積最大,則底面△ABC的面積最大,
∵AB=2,則AC=BC時△ABC面積最大,把三棱錐P-ABC補形,得到長方體PQ,
∴∠CPQ即為PC與AB所成角,
由AB=2,得AC=$\sqrt{2}$,又PA=1,∴PC=$\sqrt{3}$,
∴cos∠CPQ=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,則∠CPQ=arccos$\frac{\sqrt{3}}{3}$.
即PC與AB所成角的大小為arccos$\frac{\sqrt{3}}{3}$;
(2)∵PA⊥平面ABC,∴PA⊥BC,又BC⊥AC,PA∩AC=A,
∴BC⊥平面PAC,則平面PBC⊥平面PAC,
過A作AT⊥PC,垂足為T,則AT⊥平面PBC,∠APT即為PA與平面PCB所成角.
由PA•AC=PC•AT,得AT=$\frac{PA•AC}{PC}$=$\frac{1×\sqrt{2}}{\sqrt{3}}=\frac{\sqrt{6}}{3}$,
∴sin∠APT=$\frac{AT}{PA}=\frac{\sqrt{6}}{3}$.
則∠APT=arcsin$\frac{\sqrt{6}}{3}$.
即PA與面PCB所成角的大小為arcsin$\frac{\sqrt{6}}{3}$.
點評 本題考查異面直線所成角及線面角的求法,考查空間想象能力和思維能力,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x-y+1=0 | B. | x-y-1=0 | C. | x-y-3=0 | D. | x-y+3=0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
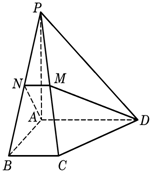 如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分別為PC、PB的中點.
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M、N分別為PC、PB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
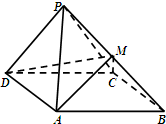 如圖,四棱錐P-ABCD中,側面PDC是邊長為2的正三角形,底面ABCD是菱形,∠ADC=60°,點P在底面ABCD上的射影為△ACD的重心,點M為線段PB上的點.
如圖,四棱錐P-ABCD中,側面PDC是邊長為2的正三角形,底面ABCD是菱形,∠ADC=60°,點P在底面ABCD上的射影為△ACD的重心,點M為線段PB上的點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com