
���}Ŀ����֪���x��R�ϵĺ���(sh��)f(x)�M��f(x��2)��f(x)���Ү�(d��ng)x��[��1��1]�r(sh��)��f(x)��x2.��g(x)��f(x)��kx��k�����څ^(q��)�g[��1��3]��(n��i)������(sh��)g(x)��0��4��(g��)����Ȍ�(sh��)�����t��(sh��)��(sh��)k��ȡֵ������(����)
A.(0������)B.![]()
C.![]() D.
D.![]()
���𰸡�C
��������
��g(x)��0����f(x)��k(x��1)������y��f(x)��[1��3]�ĈD�Ѻ���(sh��)g(x)��0��4��(g��)����Ȍ�(sh��)�����D(zhu��n)����ɂ�(g��)����(sh��)�ĈD���4��(g��)���c(di��n)�����Ô�(sh��)�νY(ji��)�Ϸ���������⣬�õ���.
���}�⣬����(sh��)g(x)��f(x)��kx��k����g(x)��0����f(x)��k(x��1)��
���ɺ���(sh��)f(x)�M��f(x��2)��f(x)���tf(x)�����ڞ�T��2��
����y��f(x)��[-1��3]�ĈD����D��ʾ��
��(d��ng)ֱ��y��k1(x��1)��(j��ng)�^(gu��)�c(di��n)(3��1)���tk1��![]() .
.
��?y��n)�ֱ��y��k(x��1)��(j��ng)�^(gu��)���c(di��n)(��1��0)�������}��ֱ֪��y��k(x��1)�cy��f(x)�ĈD����4��(g��)���c(di��n)������0<k��![]() .
.
���xC.




| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪ ���t����
���t����![]() ǡ��2��(g��)��ͬ�Č�(sh��)������(sh��)��(sh��)
ǡ��2��(g��)��ͬ�Č�(sh��)������(sh��)��(sh��)![]() ȡֵ����__________________.
ȡֵ����__________________.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() :
:![]() ��
��![]() ���ϙM����(bi��o)��4���c(di��n)�����c(di��n)�ľ��x��5��
���ϙM����(bi��o)��4���c(di��n)�����c(di��n)�ľ��x��5��
��1�����タ![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)ֱ��![]() �c���タ
�c���タ![]() ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)![]() �����M��
�����M��![]() ���C��ֱ��
���C��ֱ��![]() ���^(gu��)���c(di��n)����������c(di��n)
���^(gu��)���c(di��n)����������c(di��n)![]() ������(bi��o)��
������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ʾ��![]() ��
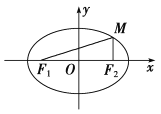
��![]() �քe��E�A�����ҽ��c(di��n)���E�A���c(di��n)
�քe��E�A�����ҽ��c(di��n)���E�A���c(di��n)![]() �ęM����(bi��o)�����ҽ��c(di��n)�ęM����(bi��o)����v����(bi��o)���ڶ̰��S�L(zh��ng)��
�ęM����(bi��o)�����ҽ��c(di��n)�ęM����(bi��o)����v����(bi��o)���ڶ̰��S�L(zh��ng)��![]() ���t�E�A���x���ʞ飨 ��
���t�E�A���x���ʞ飨 ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�����
�У�����![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ��
��![]() ��ƽ��
��ƽ��![]() ����
����![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ����
����![]() �ϵ��c(di��n)��
�ϵ��c(di��n)��![]() ��
��![]() ��
��![]() ��
��
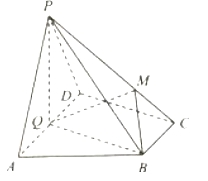
��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)��ӑՓ
�r(sh��)��ӑՓ![]() �Č�(d��o)����(sh��)
�Č�(d��o)����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
��2����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��������
��������![]() �c
�c![]() ��
��![]() ̎����ͬ���о�.
̎����ͬ���о�.
������(sh��)��(sh��)![]() ��ֵ��
��ֵ��
�������C��![]() ��
��![]() �Ϻ������
�Ϻ������
����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �څ^(q��)�g
�څ^(q��)�g![]() ��(n��i)��(sh��)���Ă�(g��)��(sh��).
��(n��i)��(sh��)����(g��)��(sh��).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��![]() �ǡ�
�ǡ�![]() ��ֱ����
��ֱ����![]() �ǡ�
�ǡ�![]() ���о���
�����![]() ����
����![]() ��E���^(gu��)E����c
��E���^(gu��)E����c![]() ����D.
����D.
��I�����C��![]() ��
��
��II����![]() ��
��![]() ����
����![]() ���L(zh��ng).
���L(zh��ng).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
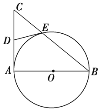
���}Ŀ����֪�AG:x2+y2-x-![]() y=0,��(j��ng)�^(gu��)�E�A
y=0,��(j��ng)�^(gu��)�E�A![]() ���ҽ��c(di��n)F������c(di��n)B,�^(gu��)�A��һ�c(di��n)(m,0)(m>a)�҃Aб�Ǟ�
���ҽ��c(di��n)F������c(di��n)B,�^(gu��)�A��һ�c(di��n)(m,0)(m>a)�҃Aб�Ǟ�![]() ��ֱ��l���E�A��C,D���c(di��n).
��ֱ��l���E�A��C,D���c(di��n).
��1����E�A�ķ���;
��2�����ҽ��c(di��n)F���Ծ���CD��ֱ���ĈAE�ă�(n��i)��,��m��ȡֵ����.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com