
【題目】如圖,![]() 是⊙
是⊙![]() 的直徑,
的直徑,![]() 是⊙
是⊙![]() 的切線,
的切線,![]() 交⊙
交⊙![]() 于E,過E的切線與
于E,過E的切線與![]() 交于D.
交于D.
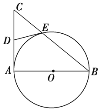
(I)求證:![]() ;
;
(II)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(I)證明見解析;(II)![]() .
.
【解析】
(I)連接![]() ,根據弦切角等于所夾的弧所對的圓周角,證得
,根據弦切角等于所夾的弧所對的圓周角,證得![]() ,由此證得
,由此證得![]() ,根據同角的余角相等,證得
,根據同角的余角相等,證得![]() ,由此證得
,由此證得![]() ,從而證得
,從而證得![]() .(II)根據勾股定理和切割線定理列方程,解方程求得
.(II)根據勾股定理和切割線定理列方程,解方程求得![]() 的長,進而求得
的長,進而求得![]() 的長.
的長.
(I)證明:
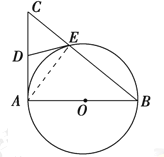
如圖,連接AE,
∵AB是⊙O的直徑,
AC,DE均為⊙O的切線,
∴∠AEC=∠AEB=90°,
∠DAE=∠DEA=∠B,
∴DA=DE.
∠C=90°-∠B=90°-∠DEA=∠DEC,
∴DC=DE,
∴CD=DA.
(II)∵CA是⊙O的切線,AB是直徑,
∴∠CAB=90°,
由勾股定理得CA2=CB2-AB2,
又CA2=CE×CB,CE=1,![]() ,
,
∴1·CB=CB2-2,
即CB2-CB-2=0,解得CB=2,
∴CA2=1×2=2,∴![]()
由(I)知D是![]() 中點,
中點,
所以DE的長為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】海關對同時從![]() 三個不同地區進口的某種商品進行抽樣檢測,從各地區進口此種商品的數量(單位:件)如下表所示,工作人員用分層抽樣的方法從這些商品中共抽取6件進行檢測.
三個不同地區進口的某種商品進行抽樣檢測,從各地區進口此種商品的數量(單位:件)如下表所示,工作人員用分層抽樣的方法從這些商品中共抽取6件進行檢測.
地區 |
|
|
|
數量 | 50 | 150 | 100 |
(1)求這6件樣品中來自![]() 各地區商品的數量;
各地區商品的數量;
(2)若在這6件樣品中隨機抽取2件送往甲機構進一步檢測,求這2件商品來自相同地區的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)滿足f(x+2)=f(x),且當x∈[-1,1]時,f(x)=x2.令g(x)=f(x)-kx-k,若在區間[-1,3]內,函數g(x)=0有4個不相等實根,則實數k的取值范圍是( )
A.(0,+∞)B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,過點
,過點![]() 的橢圓
的橢圓![]() 的兩條切線相互垂直.
的兩條切線相互垂直.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)在橢圓![]() 上是否存在這樣的點
上是否存在這樣的點![]() ,過點
,過點![]() 引拋物線
引拋物線![]() 的兩條切線
的兩條切線![]() ,切點分別為
,切點分別為![]() ,且直線
,且直線![]() 過點
過點![]() ?若存在,指出這樣的點
?若存在,指出這樣的點![]() 有幾個(不必求出點的坐標);若不存在,請說明理由.
有幾個(不必求出點的坐標);若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓過定點![]() ,且與直線
,且與直線![]() 相切.
相切.
(1)求動圓的圓心軌跡![]() 的方程;
的方程;
(2)是否存在直線![]() ,使
,使![]() 過點(0,1),并與軌跡
過點(0,1),并與軌跡![]() 交于
交于![]() 兩點,且滿足
兩點,且滿足![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠產生的廢氣經過過濾后排放,規定排放時污染物的殘留含量不得超過1%.已知在過濾過程中的污染物的殘留數量P(單位:毫克/升)與過濾時間t(單位:小時)之間的函數關系為:![]() (
(![]() 為正常數,
為正常數,![]() 為原污染物數量).若前5個小時廢氣中的污染物被過濾掉了90%,那么要能夠按規定排放廢氣,至少還需要過濾( )
為原污染物數量).若前5個小時廢氣中的污染物被過濾掉了90%,那么要能夠按規定排放廢氣,至少還需要過濾( )
A. ![]() 小時B.
小時B. ![]() 小時C. 5小時D.
小時C. 5小時D. ![]() 小時
小時
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度).設該蓄水池的底面半徑為r米,高為h米,體積為V立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12000π元(π為圓周率).
(1)將V表示成r的函數V(r),并求該函數的定義域;
(2)討論函數V(r)的單調性,并確定r和h為何值時該蓄水池的體積最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】影響消費水平的原因很多,其中重要的一項是工資收入.研究這兩個變量的關系的一個方法是通過隨機抽樣的方法,在一定范圍內收集被調查者的工資收入和他們的消費狀況.下面的數據是某機構收集的某一年內上海、江蘇、浙江、安徽、福建五個地區的職工平均工資與城鎮居民消費水平(單位:萬元).
地區 | 上海 | 江蘇 | 浙江 | 安徽 | 福建 |
職工平均工資 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城鎮居民消費水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江蘇、浙江、安徽三個地區的職工平均工資和他們的消費水平,求出線性回歸方程![]() ,其中
,其中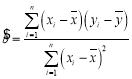
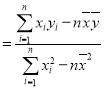 ,
,![]() ;
;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過1萬,則認為得到的線性回歸方程是可靠的,試問所得的線性回歸方程是否可靠?(![]() 的結果保留兩位小數)
的結果保留兩位小數)
(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com