【題目】為了了解手機品牌的選擇是否和年齡的大小有關，隨機抽取部分華為手機使用者和蘋果機使用者進行統計，統計結果如下表：
年齡 手機品牌 | 華為 | 蘋果 | 合計 |
30歲以上 | 40 | 20 | 60 |
30歲以下（含30歲） | 15 | 25 | 40 |
合計 | 55 | 45 | 100 |
附：
P（ | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根據表格計算得
的觀測值
，據此判斷下列結論正確的是（ ）
A.沒有任何把握認為“手機品牌的選擇與年齡大小有關”
B.可以在犯錯誤的概率不超過0.001的前提下認為“手機品牌的選擇與年齡大小有關”
C.可以在犯錯誤的概率不超過0.01的前提下認為“手機品牌的選擇與年齡大小有關”
D.可以在犯錯誤的概率不超過0.01
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，且過點
.
（1）求橢圓E的標準方程；
（2）問：是否存在過點
的直線l，使以直線l被橢圓E所截得的弦
為直徑的圓過點
，若存在，求出直線l的方程；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校針對校食堂飯菜質量開展問卷調查，提供滿意與不滿意兩種回答，調查結果如下表（單位：人）：
學生 | 高一 | 高二 | 高三 |
滿意 | 500 | 600 | 800 |
不滿意 | 300 | 200 | 400 |
（1）求從所有參與調查的人中任選1人是高三學生的概率；
（2）從參與調查的高三學生中，用分層抽樣的方法抽取6人，在這6人中任意選取2人，求這兩人對校食堂飯菜質量都滿意的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某旅游區每年各個月份接待游客的人數近似地滿足周期性規律，因而，第
個月從事旅游服務工作的人數
可近似地用函數
來刻畫，其中，正整數表示月份，
為正整數，
.
統計發現，該地區每年各個月份從事旅游服務工作的人數有以下規律：
（i）每年相同的月份，該地區從事旅游服務工作的人數基本相同；
（ii）該地區從事旅游服務工作的人數最多的8月份和最少的2月份相差約400人；
（iii）2月份該地區從事旅游服務工作的人數約為100人，隨后逐月遞增直到8月份達到最多.
（1）根據已知信息，試確定一個符合條件的的表達式.
（2）一般地，當該地區從事旅游服務工作的人數在400或400以上時，該地區也進入了一年中的旅游“旺季”.求一年中的哪幾個月是該地區的旅游旺季？請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，橢圓
的左焦點為
，過點的直線交橢圓于
，
兩點，
的最大值為
，
的最小值為
，滿足
.
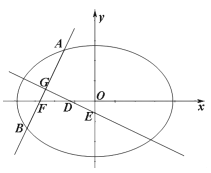
（1）若線段
垂直于軸時，
，求橢圓的方程；
（2）設線段的中點為
，的垂直平分線與
軸和
軸分別交于
，
兩點，
是坐標原點，記
的面積為
，
的面積為
，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設{an}和{bn}是兩個等差數列,記cn=max{b1-a1n,b2-a2n,…,bn-ann}(n=1,2,3,…),其中max{x1,x2,…,xs}表示x1,x2,…,xs這s個數中最大的數.
(Ⅰ)若an=n,bn=2n-1,求c1,c2,c3的值,并證明{cn}是等差數列;
(Ⅱ)證明:或者對任意正數M,存在正整數m,當n≥m時, 
>M;或者存在正整數m,使得cm,cm+1,cm+2,…是等差數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
