
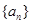 :
: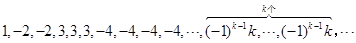 ,即當(dāng)
,即當(dāng)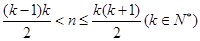 時(shí),記
時(shí),記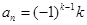 .記
.記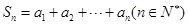 . 對于
. 對于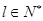 ,定義集合
,定義集合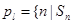 是
是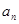 的整數(shù)倍,
的整數(shù)倍,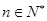 ,且
,且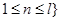 .
.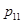 中元素的個(gè)數(shù);
中元素的個(gè)數(shù);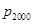 中元素的個(gè)數(shù).
中元素的個(gè)數(shù).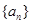 的定義,得
的定義,得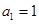 ,
,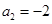 ,
,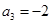 ,
,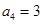 ,
,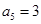 ,
,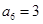 ,
,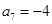 ,
,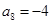 ,
,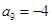 ,
,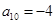 ,
,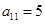 ,∴
,∴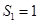 ,
,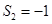 ,
,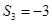 ,
,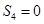 ,
,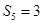 ,
,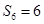 ,
,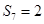 ,
,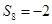
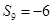 ,
,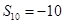 ,
,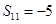 ,
,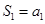 ,
,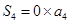 ,
,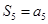 ,
,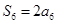 ,
,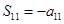 ,
,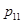 中元素的個(gè)數(shù)為5.
中元素的個(gè)數(shù)為5.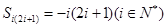 ,
,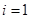 時(shí),
時(shí),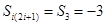 ,
,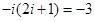 ,原等式成立;
,原等式成立;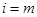 時(shí)成立,即
時(shí)成立,即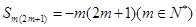 ,
,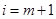 時(shí),
時(shí),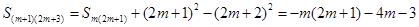
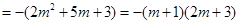 ,
,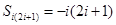 ,于是,
,于是,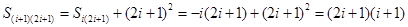 ,
,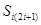 是
是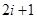 的倍數(shù),而
的倍數(shù),而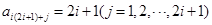 ,
,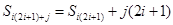 是
是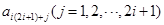 的倍數(shù),
的倍數(shù),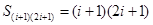 不是
不是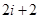 的倍數(shù),
的倍數(shù),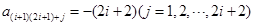 ,
,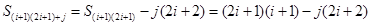 不是
不是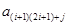
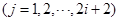 的倍數(shù),
的倍數(shù),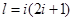 時(shí),集合
時(shí),集合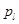 中元素的個(gè)數(shù)為
中元素的個(gè)數(shù)為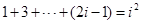 ,
,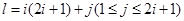 時(shí),集合
時(shí),集合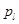 中元素的個(gè)數(shù)為
中元素的個(gè)數(shù)為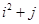 ,
,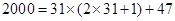 ,故集合
,故集合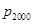 中元素的個(gè)數(shù)為
中元素的個(gè)數(shù)為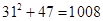 .
.

 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
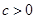 ,定義函數(shù)
,定義函數(shù)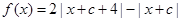 ,數(shù)列
,數(shù)列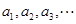 滿足
滿足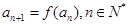 .
.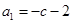 ,求
,求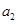 及
及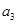 ;
;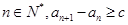 ,;
,;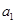 ,使得
,使得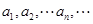 成等差數(shù)列?若存在,求出所有這樣的
成等差數(shù)列?若存在,求出所有這樣的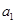 ,若不存在,說明理由.
,若不存在,說明理由.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
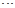 ,一直數(shù)到2013時(shí),對應(yīng)的指頭是 (填指頭的名稱).
,一直數(shù)到2013時(shí),對應(yīng)的指頭是 (填指頭的名稱). 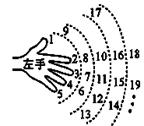
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
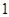 的梯形形狀.稱數(shù)列
的梯形形狀.稱數(shù)列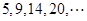 為“梯形數(shù)”.根據(jù)圖形的構(gòu)成,數(shù)列第
為“梯形數(shù)”.根據(jù)圖形的構(gòu)成,數(shù)列第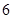 項(xiàng)
項(xiàng) ;第
;第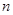 項(xiàng)
項(xiàng) .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com