
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{39}}{26}$ |
分析 根據平面向量數量積的定義公式求向量夾角的余弦值即可.
解答 解:∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夾角為$\frac{π}{3}$的單位向量,
∴$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=1×1×cos$\frac{π}{3}$=$\frac{1}{2}$,
|$\overrightarrow{a}$|=|$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$|=$\sqrt{{\overrightarrow{{e}_{1}}}^{2}+6\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{9\overrightarrow{{e}_{2}}}^{2}}$=$\sqrt{1+6×\frac{1}{2}+9}$=$\sqrt{13}$,
|$\overrightarrow{b}$|=|2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$|=$\sqrt{{4\overrightarrow{{e}_{1}}}^{2}-4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}{+\overrightarrow{{e}_{2}}}^{2}}$=$\sqrt{4-4×\frac{1}{2}+1}$=$\sqrt{3}$,
$\overrightarrow{a}$•$\overrightarrow{b}$=($\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)•(2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$)=2${\overrightarrow{{e}_{1}}}^{2}$+5$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$-3${\overrightarrow{{e}_{2}}}^{2}$=2×1+5×$\frac{1}{2}$-3×1=$\frac{3}{2}$;
∴向量$\overrightarrow{a}$與$\overrightarrow{b}$夾角θ的余弦值為:
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{\frac{3}{2}}{\sqrt{13}×\sqrt{3}}$=$\frac{\sqrt{39}}{26}$.
故選:D.
點評 本題考查了平面向量數量積的定義與應用問題,是基礎題目.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:選擇題
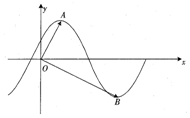 已知函數f(x)=Msin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分圖象如下圖所示,其中A,B分別為函數f(x)圖象的一個最高點和最低點,且A,B兩點的橫坐標分別為1,4,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,則函數f(x)的一個單調減區間為( )
已知函數f(x)=Msin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分圖象如下圖所示,其中A,B分別為函數f(x)圖象的一個最高點和最低點,且A,B兩點的橫坐標分別為1,4,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,則函數f(x)的一個單調減區間為( )| A. | (-6,-3) | B. | (6,9) | C. | (7,10) | D. | (10,13) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
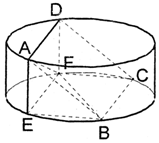 如圖,圓柱的高為2,底面半徑為3,AE,DF是圓柱的兩條母線,B、C是下底面圓周上的兩點,已知四邊形ABCD是正方形.
如圖,圓柱的高為2,底面半徑為3,AE,DF是圓柱的兩條母線,B、C是下底面圓周上的兩點,已知四邊形ABCD是正方形.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
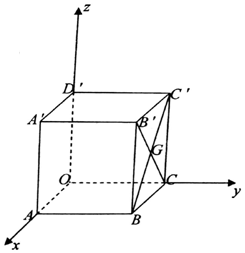 如圖,棱長為1的正方體OABC-D′A′B′C′中,G為側面正方形BCC′B′的中心,以頂點O為坐標原點建立如圖所示的空間直角坐標系,則點G的坐標為($\frac{1}{2}$,1,$\frac{1}{2}$).
如圖,棱長為1的正方體OABC-D′A′B′C′中,G為側面正方形BCC′B′的中心,以頂點O為坐標原點建立如圖所示的空間直角坐標系,則點G的坐標為($\frac{1}{2}$,1,$\frac{1}{2}$).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com