
分析 (1)利用平方關系,和加減消元法,消參可得曲線C和直線l在直角坐標系下的普通方程;
(2)若P點的坐標為P(2,1),則直線l的參數方程化為標準方程:$\left\{{\begin{array}{l}{x=2+\frac{{\sqrt{3}}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}}\right.$(t為參數),代入橢圓方程,由韋達定理,可得答案.
解答 解:(1)由題意得曲線C的參數方程為$\left\{\begin{array}{l}x=\sqrt{2}cosθ\\ y=sinθ\end{array}\right.⇒\left\{\begin{array}{l}\frac{x}{{\sqrt{2}}}=cosθ\;①\\ y=sinθ\;②\end{array}\right.$,①2+②2,得$\frac{x^2}{2}+{y^2}=1$,
所以曲線C的標準方程為:$\frac{x^2}{2}+{y^2}=1$…..…(3分)
直線l的標準方程為:$x-\sqrt{3}y-2+\sqrt{3}=0$…..…(5分)
(2)將直線l的參數方程化為標準方程:$\left\{{\begin{array}{l}{x=2+\frac{{\sqrt{3}}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}}\right.$(t為參數),…(7分)
代入橢圓方程得:$5{t^2}+8(\sqrt{3}+1)t+16=0$,
所以$|{PA}|•|{PB}|=|{{t_1}{t_2}}|=\frac{16}{5}$….…(10分)
點評 本題考查的知識點是參數方程與普通方程的互化,直線與橢圓的綜合應用,難度中檔.


科目:高中數學 來源: 題型:選擇題
| A. | [-$\frac{1}{6}$,$\frac{1}{6}$] | B. | [-$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{6}}{6}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
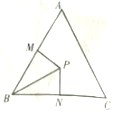 如圖,△ABC三個內角A,B,C所對的邊分別為a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC內取一點P,使得PB=3,過點P分別作直線BA,BC的垂線PM,PN,垂足分別是M,N,則|PM|+|PN|的最大值為3.
如圖,△ABC三個內角A,B,C所對的邊分別為a,b,c,已知C=$\frac{π}{3}$,$\frac{a}{b}$=$\frac{cosB}{cosA}$,在△ABC內取一點P,使得PB=3,過點P分別作直線BA,BC的垂線PM,PN,垂足分別是M,N,則|PM|+|PN|的最大值為3.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com