
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,四邊形ABCD為正方形,AB=PA=4,A點(diǎn)在PD上的射影為G點(diǎn),E點(diǎn)在AB上,平面PCE⊥平面PCD. 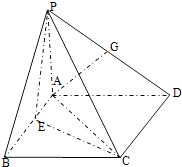
(1)求證:AG⊥平面PCD;
(2)求直線PD與平面PCE所成角的正弦值.
【答案】
(1)證明:∵CD⊥AD,CD⊥PA,AD∩PA=A
∴CD⊥平面PAD∴CD⊥AG,
又PD⊥AG,CD∩PD=D
∴AG⊥平面PCD
(2)解:如圖建立坐標(biāo)系,則P(0,0,3),C(4,4,0),D(0,4,0),G(0,2,2),
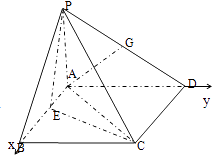
設(shè)E(a,0,0),由(1)知: ![]() 是面PCD的法向量,
是面PCD的法向量,
又 ![]() ,
, ![]() ,設(shè)面PCE的法向量為
,設(shè)面PCE的法向量為 ![]() ,
,
則 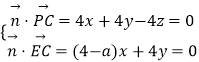 ,取x=4,得:
,取x=4,得: ![]()
因平面PCE⊥平面PCD, ![]() ,∴a=2,即:
,∴a=2,即: ![]()
又 ![]() ,設(shè)PD與面PCE所成的角為θ,
,設(shè)PD與面PCE所成的角為θ,
則: 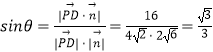
【解析】(1)先證明出CD⊥平面PAD,進(jìn)而可推斷出CD⊥AG,然后利用AG⊥PD,根據(jù)線面垂直的判定定理證明出結(jié)論.(2)建立坐標(biāo)系,先求出面PCE的法向量,再利用向量的夾角公式求出直線PD與平面PCE所成角的正弦值.
【考點(diǎn)精析】根據(jù)題目的已知條件,利用直線與平面垂直的判定和空間角的異面直線所成的角的相關(guān)知識(shí)可以得到問(wèn)題的答案,需要掌握一條直線與一個(gè)平面內(nèi)的兩條相交直線都垂直,則該直線與此平面垂直;注意點(diǎn):a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現(xiàn)了“直線與平面垂直”與“直線與直線垂直”互相轉(zhuǎn)化的數(shù)學(xué)思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點(diǎn),
上的任意兩點(diǎn),![]() 所成的角為
所成的角為![]() ,則
,則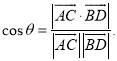 .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在△ABC中,內(nèi)角A、B、C所對(duì)的邊分別是a、b、c,且a+b+c=8.
(1)若a=2,b= ![]() ,求cosC的值;
,求cosC的值;
(2)若sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC,且△ABC的面積S=
=2sinC,且△ABC的面積S= ![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
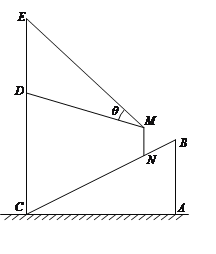
【題目】某商場(chǎng)在一部向下運(yùn)行的手扶電梯終點(diǎn)的正上方豎直懸掛一幅廣告畫(huà).如圖,該電梯的高![]() 為
為![]() 米,它所占水平地面的長(zhǎng)
米,它所占水平地面的長(zhǎng)![]() 為
為![]() 米.該廣告畫(huà)最高點(diǎn)
米.該廣告畫(huà)最高點(diǎn)![]() 到地面的距離為
到地面的距離為![]() 米,最低點(diǎn)
米,最低點(diǎn)![]() 到地面距離
到地面距離![]() 米.假設(shè)某人眼睛到腳底的距離
米.假設(shè)某人眼睛到腳底的距離![]() 為
為![]() 米,他豎直站在此電梯上觀看
米,他豎直站在此電梯上觀看![]() 視角為
視角為![]() .
.
(Ⅰ)設(shè)此人到直線![]() 的距離為
的距離為![]() 米,試用含
米,試用含![]() 的表達(dá)式表示
的表達(dá)式表示![]() ;
;
(Ⅱ)此人到直線![]() 的距離為多少米時(shí),視角
的距離為多少米時(shí),視角![]() 最大?
最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若函數(shù)f(x)=ax2﹣(2a+1)x+a+1對(duì)于任意a∈[﹣1,1],都有f(x)<0,則實(shí)數(shù)x的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某投資公司計(jì)劃投資A,B兩種金融產(chǎn)品,根據(jù)市場(chǎng)調(diào)查與預(yù)測(cè),A產(chǎn)品的利潤(rùn)y1與投資金額x的函數(shù)關(guān)系為y1=18﹣ ![]() ,B產(chǎn)品的利潤(rùn)y2與投資金額x的函數(shù)關(guān)系為y2=
,B產(chǎn)品的利潤(rùn)y2與投資金額x的函數(shù)關(guān)系為y2= ![]() (注:利潤(rùn)與投資金額單位:萬(wàn)元).
(注:利潤(rùn)與投資金額單位:萬(wàn)元).
(1)該公司已有100萬(wàn)元資金,并全部投入A,B兩種產(chǎn)品中,其中x萬(wàn)元資金投入A產(chǎn)品,試把A,B兩種產(chǎn)品利潤(rùn)總和表示為x的函數(shù),并寫(xiě)出定義域;
(2)在(1)的條件下,試問(wèn):怎樣分配這100萬(wàn)元資金,才能使公司獲得最大利潤(rùn)?其最大利潤(rùn)為多少萬(wàn)元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)y=Asin(ωx+φ)在一個(gè)周期內(nèi)的圖象如圖,此函數(shù)的解析式為( ) 
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
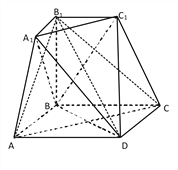
【題目】如圖所示的幾何體是由棱臺(tái)![]() 和棱錐
和棱錐![]() 拼接而成的組合體,其底面四邊形
拼接而成的組合體,其底面四邊形![]() 是邊長(zhǎng)為
是邊長(zhǎng)為![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求證:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ex﹣e﹣x+4sin3x+1,x∈(﹣1,1),若f(1﹣a)+f(1﹣a2)>2成立,則實(shí)數(shù)a的取值范圍是( )
A.(﹣2,1)
B.(0,1)
C.![]()
D.(﹣∞,﹣2)∪(1,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)= ![]() cos4x+2sinxcosx﹣
cos4x+2sinxcosx﹣ ![]() sin4x.
sin4x.
(1)當(dāng)x∈[0, ![]() ]時(shí),求f(x)的最大值、最小值以及取得最值時(shí)的x值;
]時(shí),求f(x)的最大值、最小值以及取得最值時(shí)的x值;
(2)設(shè)g(x)=3﹣2m+mcos(2x﹣ ![]() )(m>0),若對(duì)于任意x1∈[0,
)(m>0),若對(duì)于任意x1∈[0, ![]() ],都存在x2∈[0,
],都存在x2∈[0, ![]() ],使得f(x1)=g(x2)成立,求實(shí)數(shù)m的取值范圍.
],使得f(x1)=g(x2)成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com