【題目】若函數f（x）=ax2﹣（2a+1）x+a+1對于任意a∈[﹣1，1]，都有f（x）＜0，則實數x的取值范圍是 ．
【答案】（1，2）
【解析】解：函數可整理為f（x）=（x2﹣x+1）a+1﹣x ∵對于a∈[﹣1，1]時恒有f（x）＜0，
∴（x2﹣x+1）a+1﹣x＜0恒成立．
令g（a）=（x2﹣2x+1）a+1﹣x．
則函數g（a）在區間[﹣1，1]上的最大值小于0，
∵g（a）為一次函數，且一次項系數x2﹣2x+1＞0，
∴函數g（a）在區間[﹣1，1]上單調遞增，
∴g（a）max=g（1）=x2﹣2x+1+1﹣x=x2﹣3x+2＜0．
解得1＜x＜2．
所以答案是：（1，2）．
【考點精析】關于本題考查的二次函數的性質，需要了解當
時，拋物線開口向上，函數在
上遞減，在
上遞增；當
時，拋物線開口向下，函數在上遞增，在上遞減才能得出正確答案．
科目：高中數學 來源： 題型：
【題目】為貫徹“激情工作，快樂數學”的理念，某學校在學習之余舉行趣味知識有獎競賽，比賽分初賽和決賽兩部分，為了增加節目的趣味性，初賽采用選手選一題答一題的方式進行，每位選手最多有5次選答題的機會，選手累計答對3題或答錯3題即終止其初賽的比賽，答對3題者直接進入決賽，答錯3題者則被淘汰，已知選手甲答題的正確率為 
．
（1）求選手甲答題次數不超過4次可進入決賽的概率；
（2）設選手甲在初賽中答題的個數ξ，試寫出ξ的分布列，并求ξ的數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在實數集R中定義一種運算“⊙”，具有性質：①對任意a、b∈R，a⊙b=b⊙a；②a⊙0=a；③對任意a、b∈R，（a⊙b）⊙c=（ab）⊙c+（a⊙c）+（b⊙c）﹣2c，則函數f（x）=x⊙ 
的最小值是（ ）
A.2
B.3
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=lg（x+1），g（x）=lg（1﹣x）． （Ⅰ）求函數f（x）+g（x）的定義域；
（Ⅱ）判斷函數f（x）+g（x）的奇偶性，并說明理由；
（Ⅲ）判斷函數f（x）+g（x）在區間（0，1）上的單調性，并加以證明．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，PA⊥平面ABCD，四邊形ABCD為正方形，AB=PA=4，A點在PD上的射影為G點，E點在AB上，平面PCE⊥平面PCD．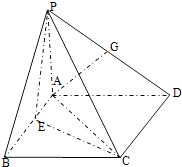 
（1）求證：AG⊥平面PCD；
（2）求直線PD與平面PCE所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）=ax﹣lnx，x∈（0，e]，其中e是自然常數，a∈R．
（1）當a=1時，求f（x）的單調區間和極值；
（2）是否存在實數a，使f（x）的最小值是3，若存在，求出a的值；若不存在，說明理由．
（3）證明：（1﹣ 
）（ 
）（ 
﹣ 
）…（ 
﹣ 
）＜e3（3﹣n） ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
