
【題目】如圖所示,在棱長為2的正方體![]() 中,
中, ![]() 分別為
分別為![]() 和
和![]() 的中點.
的中點.
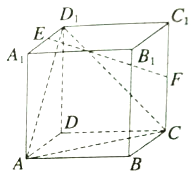
(1)求證: ![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ,若存在,求出
,若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1) 見解析(2) ![]() =
=![]()
【解析】試題分析:(1)分別以![]() 所在的直線為
所在的直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,面
,面![]() 的一個法向量是
的一個法向量是![]() ,由
,由![]() 即可證得;
即可證得;
(2)設(shè)點![]() 求解平面
求解平面![]() 的一個法向量為
的一個法向量為![]() ,平面
,平面![]() 的一個法向量
的一個法向量![]() 利用平面的法向量的夾角與二面角的大小之間的關(guān)系建立方程求解即可.
利用平面的法向量的夾角與二面角的大小之間的關(guān)系建立方程求解即可.
試題解析:
(1)證明:如圖所示,分別以![]() 所在的直線為
所在的直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,由已知得
,由已知得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∵平面![]() 的一個法向量是
的一個法向量是![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
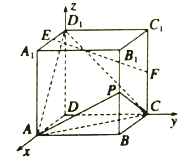
(2)解:設(shè)點![]() ,
,
平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則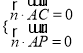 ,∵
,∵![]() ,
, ![]() ,
,
∴![]() ,取
,取![]() ,則
,則![]() ,
, ![]() ,∴
,∴![]() ,
,
平面![]() 的一個法向量
的一個法向量![]() ,
,
依題意知, ![]() 或
或![]() ,
,
∴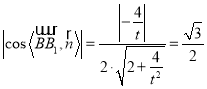 ,即
,即![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
∵![]() ,
,
∴在棱![]() 上存在一點
上存在一點![]() ,當
,當![]() 的長為
的長為![]() 時,二面角
時,二面角![]() 的大小為
的大小為![]() .
.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)判斷函數(shù)![]() 在
在![]() 的單調(diào)性.(不需要證明);
的單調(diào)性.(不需要證明);
(2)探究是否存在實數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 為奇函數(shù)?若存在,求出
為奇函數(shù)?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)在(2)的條件下,解不等式![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 和拋物線
和拋物線![]() 交于
交于![]() 兩點,且直線
兩點,且直線![]() 恰好通過橢圓
恰好通過橢圓![]() 的右焦點
的右焦點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知橢圓![]() 的左焦點為
的左焦點為![]() ,左、右頂點分別為
,左、右頂點分別為![]() ,經(jīng)過點
,經(jīng)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,記
兩點,記![]() 與
與![]() 的面積分別為
的面積分別為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)若函數(shù)![]() 有正數(shù)零點,求滿足條件的實數(shù)a的取值范圍;
有正數(shù)零點,求滿足條件的實數(shù)a的取值范圍;
(3)若對于任意的![]() 時,不等式
時,不等式![]() 恒成立,求實數(shù)x的取值范圍.
恒成立,求實數(shù)x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】分別拋擲兩顆骰子各一次,觀察向上的點數(shù),求:
(1)兩數(shù)之和為5的概率;
(2)以第一次向上的點數(shù)為橫坐標![]() ,第二次向上的點數(shù)為縱坐標
,第二次向上的點數(shù)為縱坐標![]() 的點
的點![]() 在圓
在圓![]() 內(nèi)部的概率.
內(nèi)部的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED是以BD為直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求證:AD⊥平面BFED;
(Ⅱ)在線段EF上是否存在一點P,使得平面PAB與平面ADE所成的銳二面角的余弦值為 ![]() .若存在,求出點P的位置;若不存在,說明理由.
.若存在,求出點P的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】共享單車的推廣給消費者帶來全新消費體驗,迅速贏得廣大消費者的青睞,然而,同時也暴露出管理、停放、服務(wù)等方面的問題,為了了解公眾對共享單車的態(tài)度(提倡或不提倡),某調(diào)查小組隨機地對不同年齡段50人進行調(diào)查,將調(diào)查情況整理如下表:

并且,年齡在![]() 和
和![]() 的人中持“提倡”態(tài)度的人數(shù)分別為5和3,現(xiàn)從這兩個年齡段中隨機抽取2人征求意見.
的人中持“提倡”態(tài)度的人數(shù)分別為5和3,現(xiàn)從這兩個年齡段中隨機抽取2人征求意見.
(Ⅰ)求年齡在![]() 中被抽到的2人都持“提倡”態(tài)度的概率;
中被抽到的2人都持“提倡”態(tài)度的概率;
(Ⅱ)求年齡在![]() 中被抽到的2人至少1人持“提倡”態(tài)度的概率.
中被抽到的2人至少1人持“提倡”態(tài)度的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)年齡在[20,25)中共有6人,其中持“提倡”態(tài)度的人數(shù)為5,其中抽兩人,基本事件總數(shù)n=15,被抽到的2人都持“提倡”態(tài)度包含的基本事件個數(shù)m=10,由此能求出年齡在[20,25)中被抽到的2人都持“提倡”態(tài)度的概率.(2)年齡在[40,45)中共有5人,其中持“提倡”態(tài)度的人數(shù)為3,其中抽兩人,基本事件總數(shù)n′=10,年齡在[40,45)中被抽到的2人至少1人持“提倡”態(tài)度包含的基本事件個數(shù)m′=9,由此能求出年齡在[40,45)中被抽到的2人至少1人持“提倡”態(tài)度的概率.
解析:
(1)設(shè)在![]() 中的6人持“提倡”態(tài)度的為
中的6人持“提倡”態(tài)度的為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,持“不提倡”態(tài)度的為
,持“不提倡”態(tài)度的為![]() .
.
總的基本事件有(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ).共15個,其中兩人都持“提倡”態(tài)度的有10個,
).共15個,其中兩人都持“提倡”態(tài)度的有10個,
所以P=![]() =
=![]()
(2)設(shè)在![]() 中的5人持“提倡”態(tài)度的為
中的5人持“提倡”態(tài)度的為![]() ,
, ![]() ,
, ![]() ,持“不提倡”態(tài)度的為
,持“不提倡”態(tài)度的為![]() ,
, ![]() .
.
總的基本事件有(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),(
),(![]() ),共10個,其中兩人都持“不提倡”態(tài)度的只有(
),共10個,其中兩人都持“不提倡”態(tài)度的只有(![]() )一種,所以P=
)一種,所以P=![]() =
=![]()
【題型】解答題
【結(jié)束】
22
【題目】以平面直角坐標系的原點為極點, ![]() 軸正半軸為極軸建立極坐標系,已知圓
軸正半軸為極軸建立極坐標系,已知圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),若
為參數(shù)),若![]() 與
與![]() 交于
交于![]() 兩點.
兩點.
(Ⅰ)求圓![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設(shè)![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是實數(shù),已知奇函數(shù)
是實數(shù),已知奇函數(shù)![]() ,
,
(1)求![]() 的值;
的值;
(2)若對任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0有解,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 的圖象恒過(0,0)和(1,1)兩點,則稱函數(shù)
的圖象恒過(0,0)和(1,1)兩點,則稱函數(shù)![]() 為“0-1函數(shù)”.
為“0-1函數(shù)”.
(1)判斷下面兩個函數(shù)是否是“0-1函數(shù)”,并簡要說明理由:
①![]() ; ②
; ②![]() .
.
(2)若函數(shù)![]() 是“0-1函數(shù)”,求
是“0-1函數(shù)”,求![]() ;
;
(3)設(shè)![]()
![]() ,定義在R上的函數(shù)
,定義在R上的函數(shù)![]() 滿足:① 對
滿足:① 對![]()
![]() ,
,![]()
![]() R,均有
R,均有![]() ;②
;② ![]() 是“0-1函數(shù)”,求函數(shù)
是“0-1函數(shù)”,求函數(shù)![]() 的解析式及實數(shù)a的值.
的解析式及實數(shù)a的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com