Question

13．如圖，等腰梯形ABCD中，AB∥CD，AD⊥BD，矩形ABEF所在的平面和平面ABCD相互垂直． 
（1）求證：AD⊥平面DBE；
（2）若AB=2，AD=AF=1，求三棱錐C-BDE的體積．

Answer 1

分析 （1）要證線與面垂直，需先證明直線AF垂直于平面內的兩條相交直線，因為矩形ABCD所在的平面和平面ABEF互相垂直，所以BC垂直于平面ABEF，從而AF垂直于BC，依題意，AF垂直于BF，從而得證．
（2）三棱錐E-BCD與三棱錐C-BDE的體積相等，先計算底面三角形BCD的面積，算三棱錐C-BEF的高，即為BE，最后由三棱錐體積計算公式計算即可．

解答 （1）證明：∵平面ABCD⊥平面ABEF．
平面ABCD∩平面ABEF=AB．
∵矩形ABEF．
∴EB⊥AB．∵EB?平面ABEF．
∴EB⊥平面ABCD                                           （3分）
∵AD?平面ABCD．
∵EB⊥AD，AD⊥BD，BD∩EB=B．
∴AD⊥平面BDE                                            （6分）
（2）∵AD=1，AD⊥BD，AB=2，
∴∠DAB=60°，過點C作CH⊥AB于H，則∠CBH=60°，
∴CH=$\frac{{\sqrt{3}}}{2}$，CD=AB-2HB=1，（9分）
故S_△BCD=$\frac{1}{2}$×1×$\frac{{\sqrt{3}}}{2}$=$\frac{{\sqrt{3}}}{4}$，∵EB⊥平面ABCD，
∴三棱錐E-BCD的高為EB=1，∴V_E-BCD=$\frac{1}{3}$×S_△BCD×BE=$\frac{1}{3}$×$\frac{{\sqrt{3}}}{4}$×1=$\frac{{\sqrt{3}}}{12}$（12分）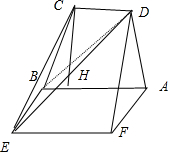

點評 本題考查了線面平行的判定，即等體積法求三棱錐的體積，屬于基礎題．