
【題目】如圖,已知四棱錐P-ABCD,△PAD是以AD為斜邊的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E為PD的中點.
(I)證明:CE∥平面PAB;
(II)求直線CE與平面PBC所成角的正弦值

【答案】(I)見解析;(II)![]() .
.
【解析】試題本題主要考查空間點、線、面位置關系,直線與平面所成的角等基礎知識,同時考查空間想象能力和運算求解能力。滿分15分。
(Ⅰ)取PA中點F,構造平行四邊形BCEF,可證明;(Ⅱ)由題意,取BC,AD的中點M,N,可得AD⊥平面PBN,即BC⊥平面PBN,過點Q作PB的垂線,垂足為H,連結MH.可知MH是MQ在平面PBC上的射影,所以∠QMH是直線CE與平面PBC所成的角.依此可在Rt△MQH中,求∠QMH的正弦值.
試題解析:
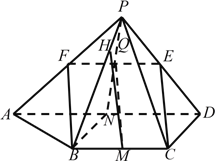
(Ⅰ)如圖,設PA中點為F,連接EF,FB.
因為E,F分別為PD,PA中點,所以![]() 且
且![]() ,
,
又因為![]() ,
, ![]() ,所以
,所以![]() 且
且![]() ,
,
即四邊形BCEF為平行四邊形,所以![]() ,
,
因此![]() 平面PAB.
平面PAB.
(Ⅱ)分別取BC,AD的中點為M,N.連接PN交EF于點Q,連接MQ.
因為E,F,N分別是PD,PA,AD的中點,所以Q為EF中點,
在平行四邊形BCEF中,MQ//CE.
由△PAD為等腰直角三角形得PN⊥AD.
由DC⊥AD,N是AD的中點得BN⊥AD.
所以AD⊥平面PBN,
由BC//AD得BC⊥平面PBN,
那么平面PBC⊥平面PBN.
過點Q作PB的垂線,垂足為H,連接MH.
MH是MQ在平面PBC上的射影,所以∠QMH是直線CE與平面PBC所成的角.
設CD=1.
在△PCD中,由PC=2,CD=1,PD=![]() 得CE=
得CE=![]() ,
,
在△PBN中,由PN=BN=1,PB=![]() 得QH=
得QH=![]() ,
,
在Rt△MQH中,QH=![]() ,MQ=
,MQ=![]() ,
,
所以sin∠QMH=![]() ,
,
所以直線CE與平面PBC所成角的正弦值是![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知以M點為圓心的圓![]() 及其上一點
及其上一點![]() .
.

(1)設圓N與y軸相切,與圓M外切,且圓心在直線![]() 上,求圓N的標準方程;
上,求圓N的標準方程;
(2)設平行于OA的直線l與圓M相交于B,C兩點且![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月,臺風“山竹”在沿海地區登陸,小張調查了當地某小區的100戶居民由于臺風造成的經濟損失,將收集到的數據分成五組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 單位:千元
單位:千元![]() ,并作出如下頻率分布直方圖
,并作出如下頻率分布直方圖

經濟損失不超過4千元 | 經濟損失超過4千元 | 合計 | |
捐款超過 500元 | 60 | ||
捐款不超 過500元 | 10 | ||
合計 |
![]() 1
1![]() 臺風后居委會號召小區居民為臺風重災區捐款,小張調查的100戶居民捐款情況如表格,在表格空白處填寫正確數字,并說明是否有
臺風后居委會號召小區居民為臺風重災區捐款,小張調查的100戶居民捐款情況如表格,在表格空白處填寫正確數字,并說明是否有![]() 以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4千元有關?
以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4千元有關?
![]() 2
2![]() 將上述調查得到的頻率視為概率,現在從該地區大量受災居民中,采用隨機抽樣的方法每次抽取一戶居民,連抽3次,記被抽取的3戶居民中自身經濟損失超過4千元的戶數為
將上述調查得到的頻率視為概率,現在從該地區大量受災居民中,采用隨機抽樣的方法每次抽取一戶居民,連抽3次,記被抽取的3戶居民中自身經濟損失超過4千元的戶數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:臨界值表:
|
|
|
|
k |
|
|
|
隨機變量:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快遞公司收取快遞費用的標準是:重量不超過![]() 的包裹收費
的包裹收費![]() 元;重量超過
元;重量超過![]() 的包裹,除
的包裹,除![]() 收費
收費![]() 元之外,超過
元之外,超過![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 計算)需再收
計算)需再收![]() 元.
元.
該公司將近![]() 天,每天攬件數量統計如下:
天,每天攬件數量統計如下:
包裹件數范圍 |
|
|
|
|
|
包裹件數 (近似處理) |
|
|
|
|
|
天數 |
|
|
|
|
|
(1)某人打算將![]() ,
, ![]() ,
, ![]() 三件禮物隨機分成兩個包裹寄出,求該人支付的快遞費不超過
三件禮物隨機分成兩個包裹寄出,求該人支付的快遞費不超過![]() 元的概率;
元的概率;
(2)該公司從收取的每件快遞的費用中抽取![]() 元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.前臺工作人員每人每天攬件不超過
元作為前臺工作人員的工資和公司利潤,剩余的作為其他費用.前臺工作人員每人每天攬件不超過![]() 件,工資
件,工資![]() 元,目前前臺有工作人員
元,目前前臺有工作人員![]() 人,那么,公司將前臺工作人員裁員
人,那么,公司將前臺工作人員裁員![]() 人對提高公司利潤是否更有利?
人對提高公司利潤是否更有利?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩品種的棉花中各抽測了25根棉花的纖維長度(單位:mm),得到如圖5的莖葉圖,整數位為莖,小數位為葉,如27.1mm的莖為27,葉為1.

(1)試比較甲、乙兩種棉花的纖維長度的平均值的大小及方差的大小;(只需寫出估計的結論,不需說明理由)
(2)將棉花按纖維長度的長短分成七個等級,分級標準如表:

試分別估計甲、乙兩種棉花纖維長度等級為二級的概率;
(3)為進一步檢驗甲種棉花的其它質量指標,現從甲種棉花中隨機抽取4根,記![]() 為抽取的棉花纖維長度為二級的根數,求
為抽取的棉花纖維長度為二級的根數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在圓![]() 上任取一點
上任取一點![]() ,過點
,過點![]() 作
作![]() 軸的垂線段,垂足為
軸的垂線段,垂足為![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,當點
,當點![]() 在圓上運動時.
在圓上運動時.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設直線![]() 與上述軌跡
與上述軌跡![]() 相交于M、N兩點,且MN的中點在直線
相交于M、N兩點,且MN的中點在直線![]() 上,求實數k的取值范圍.
上,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,過點
中,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 是邊長為
是邊長為![]() 的正方形,平面
的正方形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:面![]() 面
面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com