
【題目】某地電影院為了了解當地影迷對快要上映的一部電影的票價的看法,進行了一次調研,得到了票價x(單位:元)與渴望觀影人數y(單位:萬人)的結果如下表:
x(單位:元) | 30 | 40 | 50 | 60 |
y(單位:萬人) | 4.5 | 4 | 3 | 2.5 |
(1)若y與x具有較強的相關關系,試分析y與x之間是正相關還是負相關;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程;
(3)根據(2)中求出的線性回歸方程,預測票價定為多少元時,能獲得最大票房收入.
參考公式: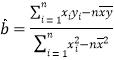 ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)當a=3時,求A∩B;
(2)若a>0,且A∩B=![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 某個集團公司下屬的甲、乙兩個企業在2014年1月的產值都為a萬元,甲企業每個月的產值與前一個月相比增加的產值相等,乙企業每個月的產值與前一個月相比增加的百分數相等,到2015年1月兩個企業的產值再次相等.
(1)試比較2014年7月甲、乙兩個企業產值的大小,并說明理由.
(2)甲企業為了提高產能,決定投入3.2萬元買臺儀器,并且從2015年2月1日起投入使用.從啟用的第一天起連續使用,第n天的維修保養費為![]() 元(n∈N*),求前n天這臺儀器的日平均耗資(含儀器的購置費),并求日平均耗資最小時使用的天數?
元(n∈N*),求前n天這臺儀器的日平均耗資(含儀器的購置費),并求日平均耗資最小時使用的天數?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在十九大會議上,黨中央明確強調“堅持房子是用來住的……”,得到了各級政府及相關單位的積極響應.在濟寧,隨著濟寧一中升學率的節節攀升,北湖校區附近的房價也在不斷攀升,為滿足廣大人民群眾的購房需求,一中北湖附近的一個樓盤開盤價已限定為每平米不超過7千元,每層每平米的價格![]() (千元)與樓層
(千元)與樓層![]() 之間符合一個二次函數的變化規律,期中一棟高33層的高層住宅最低銷售價為底層(一樓)每平米6千元,最高價為第20層每平米7千元.
之間符合一個二次函數的變化規律,期中一棟高33層的高層住宅最低銷售價為底層(一樓)每平米6千元,最高價為第20層每平米7千元.
(1)根據以上信息寫出這個二次函數的表達式![]() 及定義域.
及定義域.
(2)某單位考慮到職工子女去一中就學的實際需要,計劃團購住房,盡力爭取團購優惠政策,如果得到的優惠政策是在每套房總價的基礎上減去20(千元)后,再以余款的九五折將建筑面積為95平米的房型出售給該單位職工,張某和李某分別選定了1樓和25樓,請你根據函數性質,比較張某和李某誰獲得的優惠額度更大一些?這一優惠的額度為多少(千元)?(注:九五折--按原價的![]() 折為現價)(精確到0.001千元).
折為現價)(精確到0.001千元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年2月9-25日,第23屆冬奧會在韓國平昌舉行.4年后,第24屆冬奧會將在中國北京和張家口舉行.為了宣傳冬奧會,某大學在平昌冬奧會開幕后的第二天,從全校學生中隨機抽取了120名學生,對是否收看平昌冬奧會開幕式情況進行了問卷調查,統計數據如下:
收看 | 沒收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根據上表說明,能否有![]() 的把握認為,收看開幕式與性別有關?
的把握認為,收看開幕式與性別有關?
(Ⅱ)現從參與問卷調查且收看了開幕式的學生中,采用按性別分層抽樣的方法選取8人,參加2022年北京冬奧會志愿者宣傳活動.
(ⅰ)問男、女學生各選取多少人?
(ⅱ)若從這8人中隨機選取2人到校廣播站開展冬奧會及冰雪項目宣傳介紹,求恰好選到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率
的離心率![]() ,且圓
,且圓![]() 經過橢圓C的上、下頂點.
經過橢圓C的上、下頂點.
(1)求橢圓C的方程;
(2)若直線l與橢圓C相切,且與橢圓![]() 相交于M,N兩點,證明:
相交于M,N兩點,證明:![]() 的面積為定值(O為坐標原點).
的面積為定值(O為坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:由表中數據,求得線性回歸方程為![]() ,若從這些樣本中任取一點,則它在回歸直線左下方的概率為______.
,若從這些樣本中任取一點,則它在回歸直線左下方的概率為______.
單價 | 4 | 5 | 6 | 7 | 8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)若![]() 是
是![]() 的兩個不同零點,是否存在實數
的兩個不同零點,是否存在實數![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(2)設![]() ,函數
,函數 ,存在
,存在![]() 個零點.
個零點.
(i)求![]() 的取值范圍;
的取值范圍;
(ii)設![]() 分別是這
分別是這![]() 個零點中的最小值與最大值,求
個零點中的最小值與最大值,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com