
【題目】已知二次函數![]() .
.
(1)若![]() 是
是![]() 的兩個不同零點,是否存在實數
的兩個不同零點,是否存在實數![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(2)設![]() ,函數
,函數 ,存在
,存在![]() 個零點.
個零點.
(i)求![]() 的取值范圍;
的取值范圍;
(ii)設![]() 分別是這
分別是這![]() 個零點中的最小值與最大值,求
個零點中的最小值與最大值,求![]() 的最大值.
的最大值.
【答案】(1) 不存在.理由見解析;
(2) (i) ![]() (ii)
(ii) ![]()
【解析】
(1) .假設存在實數![]() 滿足題意,由韋達定理可得:
滿足題意,由韋達定理可得:![]()
![]() ,解得
,解得![]() ,又
,又![]() ,即
,即![]() ,綜合可得假設不成立;
,綜合可得假設不成立;
(2) (i)作出函數![]() 的圖象,觀察圖像即可求出
的圖象,觀察圖像即可求出![]() 的取值范圍;
的取值范圍;
(ii)設直線![]() 與此圖象的最左邊和最右邊的交點分別為
與此圖象的最左邊和最右邊的交點分別為![]() .即
.即![]() ,因為
,因為![]()
![]() ,代入運算可得解.
,代入運算可得解.
解:(1)依題意可知,![]() .假設存在實數
.假設存在實數![]() ,使
,使![]() 成立.
成立.
因為![]() 有兩個不同零點,.
有兩個不同零點,.
所以![]() ,解得
,解得![]() .
.
由韋達定理得![]()
所以![]()
![]()
解得![]() ,而
,而![]() ,故不存在.
,故不存在.
(2)因為![]() ,設
,設![]() ,則
,則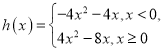 ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
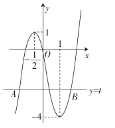
(i)作出函數![]() 的圖象,如圖所示,所以
的圖象,如圖所示,所以![]() .
.
(ii)設直線![]() 與此圖象的最左邊和最右邊的交點分別為
與此圖象的最左邊和最右邊的交點分別為![]() .
.
由![]() ,得
,得![]()
由![]() ,得
,得![]()
所以![]()
因為![]()
![]() ,
,
所以當![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.
故![]() 的最大值為
的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某地電影院為了了解當地影迷對快要上映的一部電影的票價的看法,進行了一次調研,得到了票價x(單位:元)與渴望觀影人數y(單位:萬人)的結果如下表:
x(單位:元) | 30 | 40 | 50 | 60 |
y(單位:萬人) | 4.5 | 4 | 3 | 2.5 |
(1)若y與x具有較強的相關關系,試分析y與x之間是正相關還是負相關;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程;
(3)根據(2)中求出的線性回歸方程,預測票價定為多少元時,能獲得最大票房收入.
參考公式: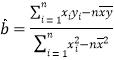 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究學生的數學核素養與抽象(能力指標![]() )、推理(能力指標
)、推理(能力指標![]() )、建模(能力指標
)、建模(能力指標![]() )的相關性,并將它們各自量化為1、2、3三個等級,再用綜合指標
)的相關性,并將它們各自量化為1、2、3三個等級,再用綜合指標![]() 的值評定學生的數學核心素養,若
的值評定學生的數學核心素養,若![]() ,則數學核心素養為一級;若
,則數學核心素養為一級;若![]() ,則數學核心素養為二級;若
,則數學核心素養為二級;若![]() ,則數學核心素養為三級,為了了解某校學生的數學核素養,調查人員隨機訪問了某校10名學生,得到如下:
,則數學核心素養為三級,為了了解某校學生的數學核素養,調查人員隨機訪問了某校10名學生,得到如下:

(1)在這10名學生中任取兩人,求這兩人的建模能力指標相同的概率;
(2)從數學核心素養等級是一級的學生中任取一人,其綜合指標為![]() ,從數學核心素養等級不是一級的學生中任取一人,其綜合指標為
,從數學核心素養等級不是一級的學生中任取一人,其綜合指標為![]() ,記隨機變量
,記隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列及其數學期望.
的分布列及其數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() =(2sinx,-1),
=(2sinx,-1),![]() ,函數f(x)=
,函數f(x)=![]() .
.
(1)求函數f(x)的對稱中心;
(2)設△ABC的內角A,B,C所對的邊為a,b,c,且a2=bc,求f(A)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】向50名學生調查對A、B兩事件的態度,有如下結果:贊成A的人數是全體的五分之三,其余的不贊成,贊成B的比贊成A的多3人,其余的不贊成;另外,對A、B都不贊成的學生數比對A、B都贊成的學生數的三分之一多1人. 問對A、B都贊成的學生有____________人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖象時,列表并填入了部分數據,如下表:
在某一個周期內的圖象時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)請將上表數據補充完整;函數![]() 的解析式為
的解析式為![]() = (直接寫出結果即可);
= (直接寫出結果即可);
(2)求函數![]() 的單調遞增區間;
的單調遞增區間;
(3)求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com